Analyzing functions: lab 3

© 2005 Ben Bolker

This lab will be somewhat shorter in terms of " R stuff" than the previous labs, because more of the new material is algebra and calculus than R commands. Try to do a reasonable amount of the work with paper and pencil before resorting to messing around in R.

derivatives ifelse for thresholds

1 Numerical experimentation: plotting curves

Here are the R commands used to generate Figure 1. They just use curve(), with add=FALSE (the default, which draws a new plot) and add=TRUE (adds the curve to an existing plot), particular values of from and to, and various graphical parameters (ylim, ylab, lty).

> curve(2 * exp(-x/2), from = 0, to = 7, ylim = c(0, 2), ylab = "")
> curve(2 * exp(-x), add = TRUE, lty = 4)
> curve(x * exp(-x/2), add = TRUE, lty = 2)
> curve(2 * x * exp(-x/2), add = TRUE, lty = 3)
> text(0.4, 1.9, expression(paste("exponential: ", 2 * e^(-x/2))), 
+     adj = 0)
> text(4, 0.7, expression(paste("Ricker: ", x * e^(-x/2))))
> text(4, 0.25, expression(paste("Ricker: ", 2 * x * e^(-x/2))), 
+     adj = 0)
> text(2.8, 0, expression(paste("exponential: ", 2 * e^(-x))))

The only new thing in this figure is the use of expression() to add a mathematical formula to an R graphic. text(x,y,"x^2") puts x^2 on the graph at position (x,y); text(x,y,expression(x^2)) (no quotation marks) puts x² on the graph. See ?plotmath or ?demo(plotmath) for (much) more information.

An alternate way of plotting the exponential parts of this curve:

> xvec = seq(0, 7, length = 100)
> exp1_vec = 2 * exp(-xvec/2)
> exp2_vec = 2 * exp(-xvec)
> plot(xvec, exp1_vec, type = "l", ylim = c(0, 2), ylab = "")
> lines(xvec, exp2_vec, lty = 4)

or, since both exponential vectors are the same length, we could cbind() them together and use matplot():

> matplot(xvec, cbind(exp1_vec, exp2_vec), type = "l", ylab = "")

Finally, if you needed to use sapply() you could say:

> expfun = function(x, a = 1, b = 1) {
+     a * exp(-b * x)
+ }
> exp1_vec = sapply(xvec, expfun, a = 2, b = 1/2)
> exp2_vec = sapply(xvec, expfun, a = 2, b = 1)

The advantage of curve() is that you don't have to define any vectors: the advantage of doing things the other way arises when you want to keep the vectors around to do other calculations with them.

Exercise 1*: Construct a curve that has a maximum at (x=5, y=1). Write the equation, draw the curve in R, and explain how you got there.

1.1 A quick digression: `ifelse()` for piecewise functions

The ifelse() command in R is useful for constructing piecewise functions. Its basic syntax is ifelse(condition,value_if_true,value_if_false), where condition is a logical vector (e.g. x>0), value_if_true is a vector of alternatives to use if condition is TRUE, and value_if_false is a vector of alternatives to use if condition is FALSE. If you specify just one value, it will be expanded (recycled in R jargon) to be the right length. A simple example:

> x = c(-25, -16, -9, -4, -1, 0, 1, 4, 9, 16, 25)
> ifelse(x < 0, 0, sqrt(x))

 [1] 0 0 0 0 0 0 1 2 3 4 5

These commands produce a warning message, but it's OK to ignore it since you know you've taken care of the problem (if you said sqrt(ifelse(x<0,0,x)) instead you wouldn't get a warning: why not?)

Here are some examples of using ifelse() to generate (1) a simple threshold; (2) a Holling type I or "hockey stick"; (3) a more complicated piecewise model that grows exponentially and then decreases linearly; (4) a double-threshold model.

> op = par(mfrow = c(2, 2), mgp = c(2, 1, 0), mar = c(4.2, 3, 1, 
+     1))
> curve(ifelse(x < 2, 1, 3), from = 0, to = 5)
> curve(ifelse(x < 2, 2 * x, 4), from = 0, to = 5)
> curve(ifelse(x < 2, exp(x), exp(2) - 3 * (x - 2)), from = 0, 
+     to = 5)
> curve(ifelse(x < 2, 1, ifelse(x < 4, 3, 5)), from = 0, to = 5)

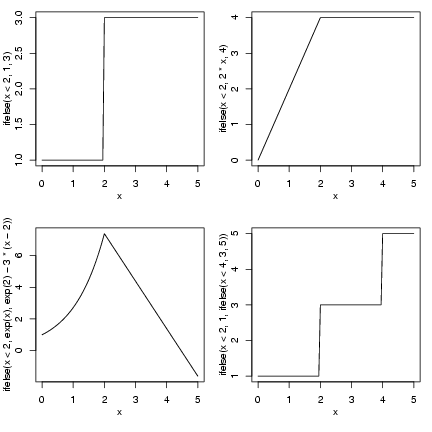The double-threshold example (nested ifelse() commands) probably needs more explanation. In words, this command would go "if x is less than 2, set y to 1; otherwise (x ł 2), if x is less than 4 (i.e. 2 Ł x < 4), set y to 3; otherwise (x ł 4), set y to 5".

2 Evaluating derivatives in R

R can evaluate derivatives, but it is not very good at simplifying them. In order for R to know that you really mean (e.g) x^2 to be a mathematical expression and not a calculation for R to try to do (and either fill in the current value of x or give an error is x is undefined), you have to specify it as expression(x^2); you also have to tell R (in quotation marks) what variable you want to differentiate with respect to:

> d1 = D(expression(x^2), "x")
> d1

2 * x

Use eval() to fill in a list of particular values for which you want a numeric answer:

> eval(d1, list(x = 2))

[1] 4

Taking the second derivative:

> D(d1, "x")

[1] 2

(As of version 2.0.1,) R knows how to take the derivatives of expressions including all the basic arithmetic operators; exponentials and logarithms; trigonometric inverse trig, and hyperbolic trig functions; square roots; and normal (Gaussian) density and cumulative density functions; and gamma and log-gamma functions. You're on your own for anything else (consider using a symbolic algebra package like Mathematica or Maple, at least to check your answers, if your problem is very complicated). deriv() is a slightly more complicated version of D() that is useful for incorporating the results of differentiation into functions: see the help page.

3 Figuring out the logistic curve

The last part of this exercise is an example of figuring out a function - Chapter 3 did this for the exponential, Ricker, and Michaelis-Menten functions The population-dynamics form of the logistic equation is

n(t) =

ć
č

n(0)

-1

ö
ř

exp(-r t)

(1)

where K is carrying capacity, r is intrinsic population growth rate, and n(0) is initial density.

At t=0, e^-rt=1 and this reduces to n(0) (as it had better!)

Finding the derivative with respect to time is pretty ugly, but it will to reduce to something you may already know. Writing the equation as n(t) = K ·(stuff)^-1 and using the chain rule we get n˘(t) = K ·(stuff)^-2 ·d(stuff)/dt (stuff=1+(K/n(0)-1)exp(-rt)). The derivative d(stuff)/dt is (K/n(0)-1) ·-r exp(-rt). At t=0, stuff=K/n(0), and d(stuff)/dt=-r(K/n(0)-1). So this all comes out to

K ·(K/n(0))^-2 ·-r (K/(n0)-1) = -r n(0)²/K ·(K/(n0)-1) = r n(0) (1-n(0)/K)

which should be reminiscent of intro. ecology: we have rediscovered, by working backwards from the time-dependent solution, that the logistic equation arises from a linearly decreasing per capita growth rate.

If n(0) is small we can do better than just getting the intercept and slope.

Exercise 2*: show that if n(0) is very small (and t is not too big), n(t) ť n(0) exp(r t). (Start by showing that K/n(0) e^-rt dominates all the other terms in the denominator.)

If t is small, this reduces (because e^rt ť 1+rt) to n(t) ť n(0) + r n(0) t, a linear increase with slope rn(0). Convince yourself that this matches the expression we got for the derivative when n(0) is small.

For large t, convince yourself tha the value of the function approaches K and (by revisiting the expressions for the derivative above) that the slope approaches zero.

The half-maximum occurs when the denominator (also known as stuff above) is 2; we can solve stuff=2 for t (getting to (K/n(0)-1) exp(-rt) = 1 and taking logarithms on both sides) to get t=log(K/n(0)-1)/r.

We have (roughly) three options:

Use curve():

> r = 1
> K = 1
> n0 = 0.1
> curve(K/(1 + (K/n0 - 1) * exp(-r * x)), from = 0, to = 10)

(note that we have to use x and not t in the expression for the logistic).

Construct the time vector by hand and compute a vector of population values using vectorized operations:

> t_vec = seq(0, 10, length = 100)
> logist_vec = K/(1 + (K/n0 - 1) * exp(-r * t_vec))
> plot(t_vec, logist_vec, type = "l")

write our own function for the logistic and use sapply():

> logistfun = function(t, r = 1, n0 = 0.1, K = 1) {
+     K/(1 + (K/n0 - 1) * exp(-r * t))
+ }
> logist_vec = sapply(t_vec, logistfun)

When we use this function, it will no longer matter how r, n0 and K are defined in the workspace: the values that R uses in logistfun() are those that we define in the call to the function.

> r = 17
> logistfun(1, r = 2)

[1] 0.4508531

> r = 0
> logistfun(1, r = 2)

[1] 0.4508531

We can do more with this plot: let's see if our conjectures are right. Using abline() and curve() to add horizontal lines to a plot to test our estimates of starting value and ending value, vertical and horizontal lines that intersect at the half-maximum, a line with the intercept and initial linear slope, and a curve corresponding to the initial exponential increase:

> curve(logistfun(x), from = 0, to = 10, lwd = 2)
> abline(h = n0, lty = 2)
> abline(h = K, lty = 2)
> abline(h = K/2, lty = 3)
> abline(v = -log(n0/(K - n0))/r, lty = 4)
> r = 1
> abline(a = n0, b = r * n0 * (1 - n0/K), lty = 5)
> curve(n0 * exp(r * x), from = 0, lty = 6, add = TRUE)

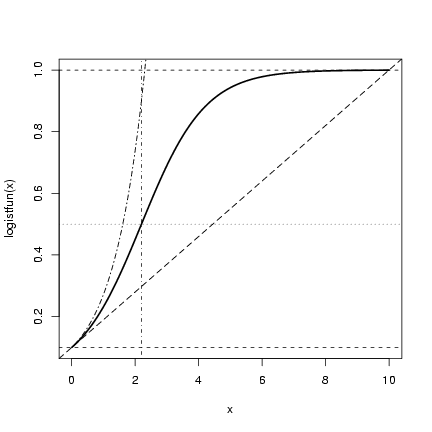Exercise 3*: Plot and analyze the function G(N)=[RN/((1+aN)^b)], (the Shepherd function), which is a generalization of the Michaelis-Menten function. What are the effects of the R and a parameters on the curve? For what parameter values does this function become equivalent to the Michaelis-Menten function? What is the behavior (value, initial slope) at N=0? What is the behavior (asymptote [if any], slope) for large N, for b=0, 0 < b < 1, b=1, b > 1? Define an R function for the Shepherd function (call it shep). Draw a plot or plots showing the behavior for the ranges above, including lines that show the initial slope. Extra credit: when does the function have a maximum between 0 and Ľ? What is the height of the maximum when it occurs? (Hint: when you're figuring out whether a fraction is zero or not, you don't have to think about the denominator at all.) The calculus isn't that hard, but you may also use the D() function in R. Draw horizontal and vertical lines onto the graph to test your answer.

Exercise 4*: Reparameterize the Holling type III functional response (f(x)=ax²/(1+bx²)) in terms of its asymptote and half-maximum.

Exercise 5*: Figure out the correspondence between the population-dynamic parameterization of the logistic function (eq. 1: parameters r, n(0), K) and the statistical parameterization (f(x)=exp(a+bx)/(1+exp(a+bx)): parameters a, b). Convince yourself you got the right answer by plotting the logistic with a=-5, b=2 (with lines), figuring out the equivalent values of K, r, and n(0), and then plotting the curve with both equations to make sure it overlaps. Plot the statistical version with lines (plot(...,type="l") or curve(...) and then add the population-dynamic version with points (points() or curve(...,type="p",add=TRUE)).

Small hint: the population-dynamic version has an extra parameter, so one of r, n(0), and K will be set to a constant when you translate to the statistical version.

Big hint: Multiply the numerator and denominator of the statistical form by exp(-a) and the numerator and denominator of the population-dynamic form by exp(rt), then compare the forms of the equations.