Lab 4: probability distributions, averaging, and Jensen's inequality
© 2005 Ben Bolker
1 Random distributions in R
R knows about lots of probability distributions. For each, it
can generate random numbers drawn from the distribution
("deviates");
compute the cumulative distribution function and the probability
distribution
function; and compute the quantile function, which gives the
x value such that ò0x P(x) dx (area under the curve from 0
to x) is a specified value, such as 0.95 (think about "tail areas"
from standard statistics).
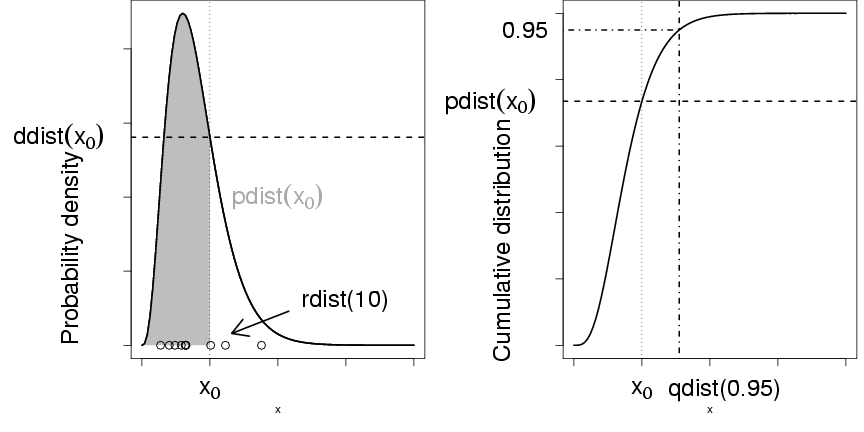 Figure 1: R functions for an arbitrary distribution
dist, showing density function (ddist),
cumulative distribution function (pdist),
quantile function (qdist), and
random-deviate function (rdist).
Let's take the binomial distribution (yet again) as an example.
Figure 1: R functions for an arbitrary distribution
dist, showing density function (ddist),
cumulative distribution function (pdist),
quantile function (qdist), and
random-deviate function (rdist).
Let's take the binomial distribution (yet again) as an example.
- rbinom(n,size,p) gives n random draws from the binomial
distribution with parameters size (total number of draws) and
p (probability of success on each draw).
You can give different parameters for each draw.
For example:
> rbinom(10, size = 8, p = 0.5)
[1] 3 6 3 4 6 7 4 3 2 2
> rbinom(3, size = 8, p = c(0.2, 0.4, 0.6))
[1] 2 4 7
Figure 2 shows the result of drawing 200 values
from a binomial distribution with N=12 and p=0.1 and
plotting the results as a factor (with 200 draws
we don't have to worry about any of the 13 possible outcomes
getting missed and excluded from the plot):
> plot(factor(rbinom(200, size = 12, p = 0.1)), xlab = "# of successes",
+ ylab = "# of trials out of 200")
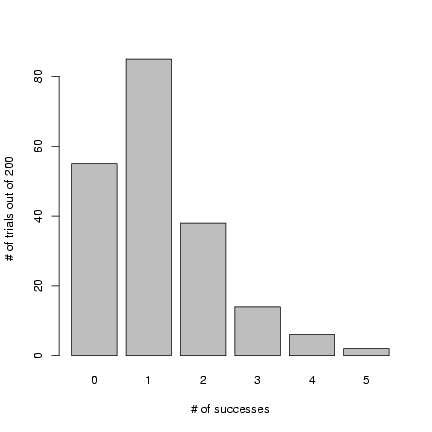 Figure 2: Results of rbinom
Figure 2: Results of rbinom
- dbinom(x,size,p) gives the value of the probability
distribution
function (pdf) at x (for a continous distribution,
the analogous function would compute the probability density
function). Since the binomial is discrete, x
has to be an integer, and the pdf is just the probability of getting
that many successes; if you try dbinom with a non-integer x, you'll get zero and a warning.
- pbinom(q,size,p) gives the value of the cumulative
distribution
function (cdf) at q (e.g. pbinom(7,size=10,prob=0.4));
- qbinom(p,size,prob) gives the quantile function,
where p is a number between 0 and 1 (an area under the pdf, or
value of the cdf) and qbinom is the value such that
P(X £ p)=q.
The quantile function Q is the inverse of the cumulative distribution
function C: if Q(p)=q then C(q)=p.
Example: qbinom(0.95,size=10,prob=0.4).
These four functions exist for each of the distributions R has built
in: e.g. for the normal distribution they're
rnorm(), pnorm(), dnorm(), qnorm().
Each distribution has its own set of parameters (so e.g. pnorm()
is pnorm(x,mean=0,sd=1)).
Exercise 1:
For the binomial distribution with 10 trials and a success probability
of 0.2:
- Pick 8 random values and sort them into increasing order
(if you set.seed(1001) beforehand, you should get X=0
(twice), X=2 (5 times), and X=4 and X=5 (once each)).
- Calculate the probabilities of getting 3, 4, or 5
successes. Answer:
[1] 0.20132659 0.08808038 0.02642412
- Calculate the probability of getting 5 or more
successes.
Answer:
[1] 0.0327935
- What tail values would you use to test against the (two-sided)
null hypothesis that p=0.2? (Use qbinom() to get the answer,
and use pbinom(0:10,size=10,prob=0.2)
and pbinom(0:10,size=10,prob=0.2,lower.tail=FALSE) to check that your
answer makes sense.
You can use the R functions to test your understanding of
a distribution and make sure that random draws match up
with the theoretical distributions as they should.
This procedure is particularly valuable when you're developing new
probability distributions by combining simpler ones,
e.g. by zero-inflating or compounding distributions.
The results of a large number of random draws should have
the correct moments (mean and variance), and a histogram
of those random draws (with freq=FALSE or prob=TRUE)
should match up with the theoretical distribution.
For example, draws from a binomial distribution with
p=0.2 and N=20 should have a mean of approximately Np=4
and a variance of Np(1-p)=3.2:
> set.seed(1001)
> N = 20
> p = 0.2
> x = rbinom(10000, prob = p, size = N)
> c(mean(x), var(x))
[1] 4.001200 3.144913
The mean is very close, the variance
is a little bit farther off.
Just for the heck of it, we can use the
replicate() function to re-do this
command many times and see how close we get:
> var_dist = replicate(1000, var(rbinom(10000, prob = p, size = N)))
(this may take a little while; if it takes too long,
lower the number of replicates to 100).
Looking at the summary statistics and
at the 2.5% and 97.5% quantiles of the
distribution of variances:
> summary(var_dist)
Min. 1st Qu. Median Mean 3rd Qu. Max.
3.052 3.169 3.199 3.199 3.229 3.340
> quantile(var_dist, c(0.025, 0.975))
2.5% 97.5%
3.114357 3.285333
(Try a histogram too.)
Even though there's some variation (of
the variance) around the theoretical value,
we seem to be doing the right thing since
the 95% confidence limits include the theoretical
value.
(Lab 5 will go into more detail on running
simulations to check the expected variation
of different measurement as a function
of parameters and sample size.)
Finally, Figure 3 shows
the entire simulated frequency distribution
along with the theoretical values.
The steps in R are:
- pick 10,000 random deviates:
> x = rbinom(10000, prob = p, size = N)
- Tabulate the values, and divide
by the number of samples to get
a probability distribution:
> tx = table(factor(x, levels = 0:12))/10000
(The levels
command is necessary in this case
because the probability of
x=12 with p=0.2 and N=12
is actually so low (8.7×10-5)
that there's a reasonable chance that
a sample of 10,000 won't include any
samples with 12 successes.)
-
Draw a barplot of the values, extending
the y-limits a bit to make room for
the theoretical values and saving the
x locations at which the bars are drawn:
> b1 = barplot(tx, ylim = c(0, 0.23), ylab = "Probability")
- Add the theoretical values, plotting them
at the same x-locations as the centers
of the bars:
> points(b1, dbinom(0:12, prob = p, size = N), pch = 16)
(barplot() doesn't put the bars
at x locations corresponding to their
numerical values, so you have to save
those values as b1 and re-use
them to make sure the theoretical
values end up in the right place.)
A few alternative ways to do this plot would be:
-
> plot(factor(x))
> points(b1, 10000 * dbinom(0:12, prob = p, size = N))
(plots the number of observations without rescaling and
scales the probability distribution to match);
-
> plot(table(x)/10000)
> points(0:12, dbinom(0:12, prob = p, size = N))
Plotting a table does a plot with type="h" (high
density), which plots a vertical line for each value.
I think it's not quite as pretty as the barplot, but
it works.
Unlike factors, tables can be scaled numerically,
and the lines end up at the right numerical locations,
so we can just use 0:12 as the x locations
for the theoretical values.
- You could also draw a histogram:
since histograms were really designed
continuous data you have to make sure the
breaks occur in the right place (halfway
between counts):
> h = hist(x, breaks = seq(-0.5, 12.5, by = 1), col = "gray", prob = TRUE)
> points(0:12, dbinom(0:12, prob = p, size = N))
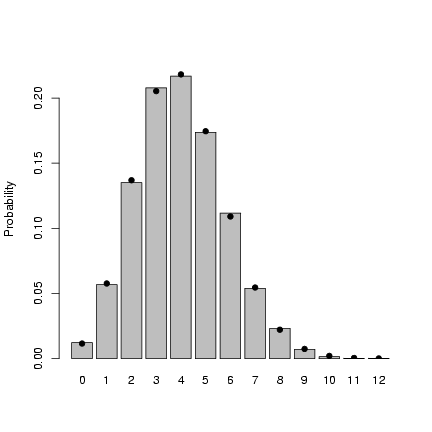 Figure 3: Checking binomial deviates against
theoretical values.
Doing the equivalent plot for continuous distributions
is actually somewhat easier, since you don't have
to deal with the complications of a discrete distribution:
just use hist(...,prob=TRUE) to show the
sampled distribution (possibly with ylim
adjusted for the maximum of the theoretical
density distribution) and
ddist(x,[parameters],add=TRUE) to add the
theoretical curve
(e.g.: curve(dgamma(x,shape=2,scale=1,add=FALSE))).
Exercise 2*:
Pick 10,000 negative binomial
deviates with m = 2, k=0.5.
Pick one of the ways above to draw
the distribution.
Check that the mean and variance
agree reasonably well with the theoretical values.
Add points representing
the theoretical distribution to the plot.
Now translate the m and k
parameters into their p and nn
equivalents (the coin-flipping derivation
of the negative binomial), and add
those points to the plot [use a different
plotting symbol to make sure you can see
that they overlap with the theoretical
values based on the m, k parameterization].
Figure 3: Checking binomial deviates against
theoretical values.
Doing the equivalent plot for continuous distributions
is actually somewhat easier, since you don't have
to deal with the complications of a discrete distribution:
just use hist(...,prob=TRUE) to show the
sampled distribution (possibly with ylim
adjusted for the maximum of the theoretical
density distribution) and
ddist(x,[parameters],add=TRUE) to add the
theoretical curve
(e.g.: curve(dgamma(x,shape=2,scale=1,add=FALSE))).
Exercise 2*:
Pick 10,000 negative binomial
deviates with m = 2, k=0.5.
Pick one of the ways above to draw
the distribution.
Check that the mean and variance
agree reasonably well with the theoretical values.
Add points representing
the theoretical distribution to the plot.
Now translate the m and k
parameters into their p and nn
equivalents (the coin-flipping derivation
of the negative binomial), and add
those points to the plot [use a different
plotting symbol to make sure you can see
that they overlap with the theoretical
values based on the m, k parameterization].
2 Averaging across discrete and continuous distributions
Suppose we have a (tiny) data set;
we can organize it in two different ways,
in standard long format or in tabular form:
> dat = c(5, 6, 5, 7, 5, 8)
> dat
[1] 5 6 5 7 5 8
> tabdat = table(dat)
> tabdat
dat
5 6 7 8
3 1 1 1
To get the (sample) probability distribution of the data,
just scale by the total sample size:
> prob = tabdat/length(dat)
> prob
dat
5 6 7 8
0.5000000 0.1666667 0.1666667 0.1666667
(dividing by sum(tabdat) would
be equivalent).
In the long format, we can take
the mean with mean(dat)
or, replicating the formula åxi/N
exactly, sum(dat)/length(dat).
In the tabular format, we
can calculate the mean
with the formula åP(x) x,
which in R would be
sum(prob*5:8) or
more generally
> vals = as.numeric(names(prob))
> sum(prob * vals)
[1] 6
(you could also get the values
by as.numeric(levels(prob)),
or by sort(unique(dat))).
However, mean(prob)
or mean(tabdat) is just plain wrong
(at least, I can't think of a situation where
you would want to calculate this value).
Exercise 3: figure out
what it means that
mean(tabdat) equals 1.5.
Going back the other way, from a table to raw values, we can use
the rep() function to repeat values an appropriate number of times.
In its simplest form, rep(x,n) just creates
a vector repeats x (which
may be either a single value or a vector) n times, but
if n is a vector as well then each element of x
is repeated the corresponding number of times: for example,
> rep(c(1, 2, 3), c(2, 1, 5))
[1] 1 1 2 3 3 3 3 3
gives two copies of 1, one copy of 2, and five copies of 3.
Therefore,
> rep(vals, tabdat)
[1] 5 5 5 6 7 8
will recover our original data (although not in the original
order) by repeating each element of vals
the correct number of times.
2.1 Jensen's inequality
Looking at Schmitt et al's data, the recruitment level very
nearly fits an exponential distribution with
a mean of 24.5 (so l = 1/24.5).
Schmitt et al. also say that recruitment (R)
as a function of settlement (S) is R = aS/(1+(a/b)S),
with a = 0.696 (initial slope, recruits per 0.1 m2 patch reef per recruit)
and b = 9.79 (asymptote, recruits per 0.1 m2 patch reef).
Let's see how strong Jensen's inequality is for this population.
We'll figure out the average by approximating an integral
by a sum: ò0¥ f(S) P(S) dS » åf(Si) P(Si) DS.
We need to set the range big enough to get most of the probability
of the distribution, and the DS small enough to get most
of the variation in the distribution; we'll try 0-200 in steps of 0.1.
(If I set the range too small or the DS too big, I'll miss
a piece of the distribution or the function. If I try to be too
precise, I'll waste time computing.)
In R:
> a = 0.696
> b = 9.79
> dS = 0.1
> S = seq(0, 200, by = dS)
> pS = dexp(S, rate = 1/24.5)
> fS = a * S/(1 + (a/b) * S)
> sum(pS * fS * dS)
[1] 5.008049
R also knows how to integrate functions numerically:
it can even approximate an integral from 0 to ¥.
First we have to define a (vectorizable) function:
> tmpf = function(S) {
+ dexp(S, rate = 1/24.5) * a * S/(1 + (a/b) * S)
+ }
Then we can just ask R to integrate it:
> i1 = integrate(tmpf, lower = 0, upper = Inf)
> i1
5.010691 with absolute error < 5.5e-05
(Use adapt(), in the adapt package,
if you need to do multidimensional integrals.)
This integral shows that we were pretty close
with our first approximation.
However, numerical integration will always
imply some level of approximation; be
careful with functions with sharp spikes,
because it can be easy to miss important parts
of the function.
Now to try out the delta function approximation:
> d1 = D(expression(a * x/(1 + (a/b) * x)), "x")
> d2 = D(d1, "x")
As stated above,
the mean value of the distribution is about 24.5.
The variance of the exponential distribution is
equal to the mean squared, or 600.25.
> Smean = 24.5
> Svar = Smean^2
> d2_num = eval(d2, list(a = 0.696, b = 9.79, x = Smean))
> mval = a * Smean/(1 + (a/b) * Smean)
> dapprox = mval + 1/2 * Svar * d2_num
> merr = (mval - i1$value)/i1$value
> merr
[1] 0.2412107
> err = (dapprox - i1$value)/i1$value
> err
[1] -0.04637931
The answer from the delta method
(f([`x])+(s2 f"([`x])/2))
is only about 5% below
the true value, as
opposed to the naive answer (f([`x])) which is about
25% high. (We have to say i1$value
to extract the actual value of the integral
from the variable i1; try str(i1)
if you want to see all the information that
R is storing about the integral.)
Exercise 4*:
try the above exercise again, but this time
with a gamma distribution instead of an exponential.
Keep the mean equal to 24.5 and change the
variance to 100, 25, and 1 (use the information
that the mean of the gamma distribution is shape*scale
and the variance is shape*scale^2).
Including the results for the exponential
(which is a gamma with shape=1), make a table
showing how the (1) true value of
mean recruitment [calculated by
numerical integration in R either
using integrate() or summing
over small DS] (2) value of
recruitment at the mean settlement
(3) delta-method approximation
(4,5) proportional error in #2 and #3
change with the variance.
3 The method of moments: reparameterizing distributions
In the chapter, I showed how to use the method of moments
to estimate the parameters of a distribution by setting the
sample mean and variance ([`x], s2) equal to the theoretical
mean and variance of a distribution and solving for the parameters.
For the negative binomial, in particular, I found m = [`x]
and k=([`x])/(s2/[`x] -1).
You can also define your own functions that use
your own parameterizations: call them my_function
rather than just replacing the standard R functions
(which will lead to insanity in the long run).
For example, defining
> my_dnbinom = function(x, mean, var, ...) {
+ mu = mean
+ k = mean/(var/mean - 1)
+ dnbinom(x, mu = mu, size = k, ...)
+ }
> my_rnbinom = function(n, mean, var, ...) {
+ mu = mean
+ k = mean/(var/mean - 1)
+ rnbinom(n, mu = mu, size = k, ...)
+ }
(the ... in the function takes any other arguments
you give to my_dnbinom and just passes them through,
unchanged, to dnbinom).
Defining your own functions can be handy if you need
to work on a regular basis with a distribution that
uses a different parameterization than the one built
into the standard R function.
You can use the kinds of histograms shown above to test your
results (remembering that the method of moments estimates
may be slightly biased especially for small samples - but
they shouldn't cause errors as large as those caused by
typical algebra mistakes).
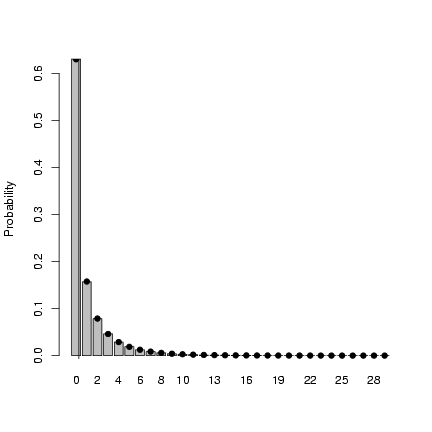
> x = my_rnbinom(1e+05, mean = 1, var = 4)
> mean(x)
[1] 0.9999
> var(x)
[1] 4.00574
> tx = table(factor(x, levels = 0:max(x)))/1e+05
> b1 = barplot(tx, ylab = "Probability")
> points(b1, my_dnbinom(0:max(x), mean = 1, var = 4), pch = 16)
> abline(v = 1)
 Exercise 5*:
Morris (1997) gives a definition of the beta function that
is different from the standard statistical parameterization.
The standard parameterization is
Exercise 5*:
Morris (1997) gives a definition of the beta function that
is different from the standard statistical parameterization.
The standard parameterization is
|
Beta(x|a,b) = |
G(a+b)
G(a)G(b)
|
xa-1(1-x)b-1 |
|
whereas Morris uses
|
Beta(x|P,q) = |
G(q)
G(qP)G(q(1-P))
|
xqP-1 (1-x)q(1-P)-1. |
|
Find expressions for P and q in terms of a and b
and vice versa. Explain why you might prefer Morris's
parameterization.
Define a new set of functions that generate random
deviates from the beta distribution (my_rbeta)
and calculate the density function (my_dbeta)
in terms of P and q.
Generate a histogram from this distribution
and draw a vertical line showing the mean of the distribution.
4 Creating new distributions
4.1 Zero-inflated distributions
The general formula for the probability distribution of
the a zero-inflated distribution, with an underlying
distribution P(x) and a zero-inflation probability
of pz, is:
So, for example, we could define a probability distribution
for a zero-inflated negative binomial as follows:
> dzinbinom = function(x, mu, size, zprob) {
+ ifelse(x == 0, zprob + (1 - zprob) * dnbinom(0, mu = mu,
+ size = size), (1 - zprob) * dnbinom(x, mu = mu, size = size))
+ }
(the name, dzinbinom, follows the R convention
for a probability distribution function: a d
followed by the abbreviated name of the distribution,
in this case zinbinom for
"zero-inflated negative
binomial").
The ifelse() command checks every element of
x to see whether it is zero or not and fills
in the appropriate value depending on the answer.
A random deviate generator would look like this:
> rzinbinom = function(n, mu, size, zprob) {
+ ifelse(runif(n) < zprob, 0, rnbinom(n, mu = mu, size = size))
+ }
The command runif(n) picks n
random values between 0 and 1; the ifelse
command compares them with the value of
zprob. If an individual value is
less than zprob (which happens with probability
zprob=pz), then the corresponding
random number is zero; otherwise it is a value
picked out of the appropriate negative binomial
distribution.
Exercise 6:
check graphically that these functions actually
work. For an extra challenge, calculate the mean
and variance of the zero-inflated negative binomial
and compare it to the results of
rzinbinom(10000,mu=4,size=0.5,zprob=0.2).
5 Compounding distributions
The key to compounding distributions in R is
that the functions that generate random deviates
can all take a vector of different parameters
rather than a single parameter. For example,
if you were simulating the number of hatchlings
surviving (with individual probability 0.8)
from a series of 8 clutches, all of size
10, you would say
> rbinom(8, size = 10, prob = 0.8)
[1] 7 6 9 7 9 9 6 8
but if you had a series of clutches
of different sizes, you could still
pick all the random values at the same time:
> clutch_size = c(10, 9, 9, 12, 10, 10, 8, 11)
> rbinom(8, size = clutch_size, prob = 0.8)
[1] 10 7 8 8 6 7 6 8
Taking this a step farther, the clutch size
itself could be a random variable:
> clutch_size = rpois(8, lambda = 10)
> rbinom(8, size = clutch_size, prob = 0.8)
[1] 7 10 7 11 13 4 5 4
We've just generated a Poisson-binomial
random deviate ...
As a second example, I'll
follow Clark et al. in constructing
a distribution that is a compounding
of normal distributions, with 1/variance of each sample drawn from
a gamma distribution.
First pick the variances as the reciprocals of 10,000 values
from a gamma distribution with shape 5 (setting the scale equal
to 1/5 so the mean will be 1):
> var_vals = 1/rgamma(10000, shape = 5, scale = 1/5)
Take the square root, since dnorm uses
the standard deviation and not the variance
as a parameter:
> sd_vals = sqrt(var_vals)
Generate 10,000 normal deviates using this
range of standard deviations:
> x = rnorm(10000, mean = 0, sd = sd_vals)
Figure 4 shows a histogram of the
following commands:
> hist(x, prob = TRUE, breaks = 100, col = "gray")
> curve(dt(x, df = 11), add = TRUE, lwd = 2)
The superimposed curve is a t distribution
with 11 degrees of freedom; it turns out that
if the underlying gamma distribution has
shape parameter p, the resulting t distribution
has df=2p+1.
(Figuring out the analytical form of the compounded
probability distribution or density function, or
its equivalence to some existing distribution,
is the hard part; for the most part, though,
you can find these answers in the ecological
and statistical literature if you search hard
enough.
> hist(x, prob = TRUE, breaks = 100, col = "gray")
> curve(dt(x, df = 11), add = TRUE, lwd = 2)
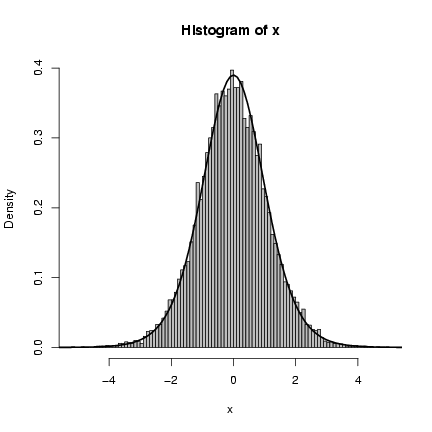 Figure 4: Clark model: inverse gamma compounded with normal,
equivalent to the Student t distribution
Exercise 7*:
generate 10,000 values from
a gamma-Poisson compounded distribution
with parameters shape=k=0.5, scale=m/k=4/0.5=8
and demonstrate that it's equivalent to a
negative binomial with the appropriate
m and k parameters.
Extra credit: generate 10,000
values from a lognormal-Poisson distribution
with the same expected mean and variance
(the variance of the lognormal should
equal the variance of the gamma distribution
you used as a compounding distribution;
you will have to do some algebra
to figure out the values of meanlog
and sdlog needed to produce a lognormal
with a specified mean and variance.
Plot the distribution and superimpose
the theoretical distribution of the
negative binomial with the same mean
and variance
to see how different the shapes of the distributions
are.
Figure 4: Clark model: inverse gamma compounded with normal,
equivalent to the Student t distribution
Exercise 7*:
generate 10,000 values from
a gamma-Poisson compounded distribution
with parameters shape=k=0.5, scale=m/k=4/0.5=8
and demonstrate that it's equivalent to a
negative binomial with the appropriate
m and k parameters.
Extra credit: generate 10,000
values from a lognormal-Poisson distribution
with the same expected mean and variance
(the variance of the lognormal should
equal the variance of the gamma distribution
you used as a compounding distribution;
you will have to do some algebra
to figure out the values of meanlog
and sdlog needed to produce a lognormal
with a specified mean and variance.
Plot the distribution and superimpose
the theoretical distribution of the
negative binomial with the same mean
and variance
to see how different the shapes of the distributions
are.
File translated from
TEX
by
TTH,
version 3.67.
On 28 Sep 2005, 13:38.



 Exercise 5*:
Morris (1997) gives a definition of the beta function that
is different from the standard statistical parameterization.
The standard parameterization is
Exercise 5*:
Morris (1997) gives a definition of the beta function that
is different from the standard statistical parameterization.
The standard parameterization is
