Lab 6: estimation
Ben Bolker
© 2005 Ben Bolker
1 Made-up data: negative binomial
The simplest thing to do to convince yourself that
your attempts to estimate parameters are working
is to simulate the "data" yourself and see if
you get close to the right answers back.
Start by making up some negative binomial "data":
first, set the random-number seed so we get
consistent results across different R sessions:
> set.seed(1001)
Generate 50 values with m = 1, k=0.4
(save the values in variables in case we
want to use them again later, or change
the parameters and run the code again):
> mu.true = 1
> k.true = 0.4
> x = rnbinom(50, mu = mu.true, size = k.true)
Take a quick look at what we got:
> plot(table(factor(x, levels = 0:max(x))), ylab = "Frequency",
+ xlab = "x")
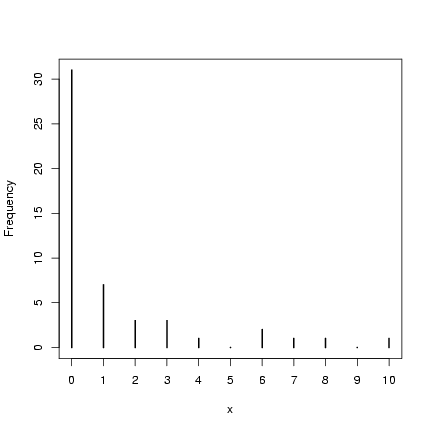(reminder: I won't always draw the pictures, but it's
good to make a habitat of examining your variables
(with summary() etc. and graphically) as you
go along to make sure you know what's going on!)
Negative log-likelihood function for a simple
draw from a negative binomial distribution:
the first parameter, p, will be the
vector of parameters, and the second parameter,
dat, will be the data vector (in case we
want to try this again later with a different
set of data; by default we'll set it to the
x vector we just drew randomly).
> NLLfun1 = function(p, dat = x) {
+ mu = p[1]
+ k = p[2]
+ -sum(dnbinom(x, mu = mu, size = k, log = TRUE))
+ }
Calculate the negative log-likelihood for the true values.
I have to combine these values into a vector with
c() to pass them to the negative
log-likelihood function.
Naming the elements in the vector is optional
but will help keep things clear as we go along:
> nll.true = NLLfun1(c(mu = mu.true, k = k.true))
> nll.true
[1] 72.64764
The NLL for other parameter values that I know are
way off (m = 10, k=10):
> NLLfun1(c(mu = 10, k = 10))
[1] 291.4351
Much higher negative log-likelihood, as it should be.
Find the method-of-moments estimates for m and k:
> m = mean(x)
> v = var(x)
> mu.mom = m
> k.mom = m/(v/m - 1)
Negative log-likelihood estimate for method of moments
parameters:
> nll.mom = NLLfun1(c(mu = mu.mom, k = k.mom))
> nll.mom
[1] 72.08996
Despite the known bias, this estimate is better (lower
negative log-likelihood) than the "true" parameter
values. The Likelihood Ratio Test would say, however,
that the difference in likelihoods would have to
be greater than c22(0.95)/2 (two degrees of
freedom because we are allowing both m and k
to change):
> ldiff = nll.true - nll.mom
> ldiff
[1] 0.5576733
> qchisq(0.95, df = 2)/2
[1] 2.995732
So - better, but not significantly better at p=0.05.
(pchisq(2*ldiff,df=2,lower.tail=FALSE) would tell us the
exact p-value if we wanted to know.)
But what is the MLE? Use optim with
the default options (Nelder-Mead simplex method)
and the method-of-moments estimates as the starting
estimates (par):
> O1 = optim(fn = NLLfun1, par = c(mu = mu.mom, k = k.mom), hessian = TRUE)
> O1
$par
mu k
1.2602356 0.2884793
$value
[1] 71.79646
$counts
function gradient
45 NA
$convergence
[1] 0
$message
NULL
$hessian
mu k
mu 7.387808331 0.004901569
k 0.004901569 97.372581408
The optimization result is a list with
elements:
- the best-fit
parameters (O1$par, with parameter names because we named the
elements of the starting vector-see how useful this is?);
- the minimum negative log-likelihood (O1$value);
- information on the number of function evaluations
(O1$counts; the gradient part is NA
because we didn't specify a function to calculate
the derivatives (and the Nelder-Mead algorithm wouldn't
have used them anyway);
- information on whether the
algorithm thinks it found a good answer
(O1$convergence, which is zero if R thinks
everything worked and uses various numeric codes
(see ?optim for details) if something goes
wrong;
- O1$message which may give further
information about the when the fit converged or
how it failed to converge;
- because we set hessian=TRUE, we also
get O1$hessian, which gives the (finite difference
approximation of) the second derivatives evaluated
at the MLE
The minimum negative log-likelihood
(71.8) is better than
either the negative log-likelihood
corresponding to the method-of-moments
parameters (72.09) or
the true parameters (72.65),
but all of these are within the LRT cutoff.
Now let's find the likelihood surface, the profiles,
and the confidence intervals.
The likelihood surface is straightforward: set up
vectors of m and k values and run for
loops, set up a matrix to hold the results, and run
for loops to calculate and store the values.
Let's try m from 0.4 to 3 in steps of 0.05 and
k from 0.01 to 0.7 in steps of 0.01.
(I initially had the m vector from 0.1 to 2.0
but revised it after seeing the contour plot below.)
> muvec = seq(0.4, 3, by = 0.05)
> kvec = seq(0.01, 0.7, by = 0.01)
The matrix for the results will have
rows corresponding to m and
columns corresponding to k:
> resmat = matrix(nrow = length(muvec), ncol = length(kvec))
Run the for loops:
> for (i in 1:length(muvec)) {
+ for (j in 1:length(kvec)) {
+ resmat[i, j] = NLLfun1(c(muvec[i], kvec[j]))
+ }
+ }
Drawing a contour: the initial default choice of contours
doesn't give us fine enough resolution (it picks contours
spaced 5 apart to cover the range of the values in the
matrix), so I added levels spaced 1 log-likelihood unit
apart from 70 to 80 by doing a second contour
plot with add=TRUE.
> contour(muvec, kvec, resmat, xlab = expression(mu), ylab = "k")
> contour(muvec, kvec, resmat, levels = 70:80, lty = 2, add = TRUE)
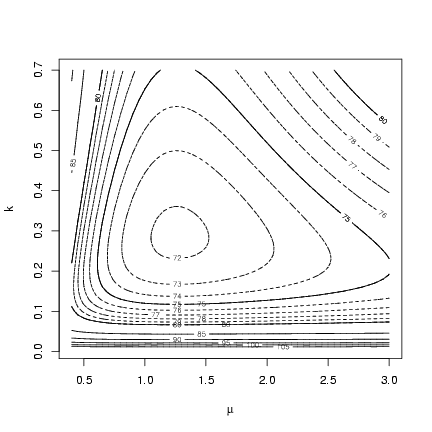Alternately, we could set the levels of the contour
plot corresponding to different 1-a levels
for the likelihood ratio test: if the minimum
negative log-likelihood is m, then these levels
are m+c22(a)/2:
> alevels = c(0.5, 0.9, 0.95, 0.99, 0.999)
> minval = O1$value
> nll.levels = qchisq(alevels, df = 2)/2 + minval
> contour(muvec, kvec, resmat, levels = nll.levels, labels = alevels,
+ xlab = expression(mu), ylab = "k")
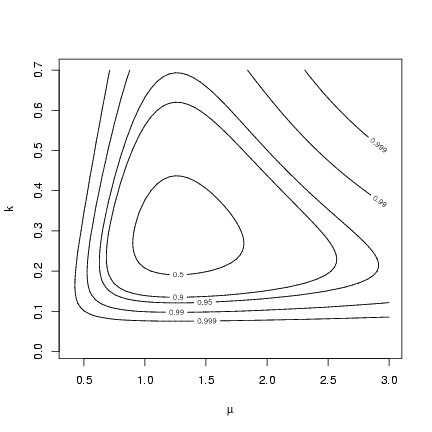So far, so good. Finding the profiles and confidence limits
is a bit harder.
To calculate the m profile, define a new function that
takes m as a separate parameter (which optim
will not try to adjust as it goes along) and optimizes with respect to k:
> NLLfun.mu = function(p, mu) {
+ k = p[1]
+ -sum(dnbinom(x, mu = mu, size = k, log = TRUE))
+ }
Set up a matrix with two columns (one for the best-fit k value,
one for the minimum negative log-likelihood achieved):
> mu.profile = matrix(ncol = 2, nrow = length(muvec))
Run a for loop, starting the optimization
from the maximum-likelihood value of k every time.
Also include the value for m (mu=muvec[i]),
which R will pass on to the function that computes
the negative log-likelihood.
The default Nelder-Mead method doesn't work well on
1-dimensional problems, and will give a warning.
I tried method="BFGS" instead
but got warnings about
NaNs produced in ... ,
because optim
tries some negative values for k
on its way to the correct (positive) answer.
I then switched to L-BFGS-B and set
lower=0.002, far enough above zero that
optim wouldn't run into any negative
numbers when it calculated the derivatives
by finite differences.
Another option would have been to change the
function around so that it minimized with
respect to log(k) instead of k. This function
would look something like:
> NLLfun.mu2 = function(p, mu) {
+ logk = p[1]
+ k = exp(logk)
+ -sum(dnbinom(x, mu = mu, size = k, log = TRUE))
+ }
and of course we would have to translate the
answers back from the log scale to compare them
to the results so far.
(The other option
would be to use optimize, a function specially
designed for 1D optimization, but this way we have
to do less rearranging of the code.)
A general comment about warnings: it's OK to
ignore warnings if you understand exactly
where they come from and have satisfied yourself
that whatever problem is causing the warnings
does not affect your answer in any significant
way. Ignoring warnings at any other time is
a good way to overlook bugs in your code or
serious problems with numerical methods that
will make your answers nonsensical.
So, anyway - run that optimization for each
value of m in the m vector.
At each step, save the parameter estimate and
the minimum negative log-likelihood:
> for (i in 1:length(muvec)) {
+ Oval = optim(fn = NLLfun.mu, par = O1$par["k"], method = "L-BFGS-B",
+ lower = 0.002, mu = muvec[i])
+ mu.profile[i, ] = c(Oval$par, Oval$value)
+ }
> colnames(mu.profile) = c("k", "NLL")
Do the same process for k:
> NLLfun.k = function(p, k) {
+ mu = p[1]
+ -sum(dnbinom(x, mu = mu, size = k, log = TRUE))
+ }
> k.profile = matrix(ncol = 2, nrow = length(kvec))
> for (i in 1:length(kvec)) {
+ Oval = optim(fn = NLLfun.k, par = O1$par["mu"], method = "L-BFGS-B",
+ lower = 0.002, k = kvec[i])
+ k.profile[i, ] = c(Oval$par, Oval$value)
+ }
> colnames(k.profile) = c("mu", "NLL")
Redraw the contour plot with profiles added:
> contour(muvec, kvec, resmat, xlab = expression(mu), ylab = "k")
> contour(muvec, kvec, resmat, levels = 70:80, lty = 2, add = TRUE)
> lines(muvec, mu.profile[, "k"], lwd = 2)
> lines(k.profile[, "mu"], kvec, lwd = 2, lty = 2)
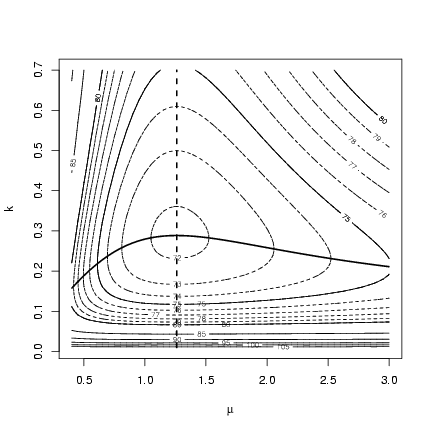The contour for m is completely independent of k:
no matter what value you choose for k, the best estimate
of m is still the same (and equal to the mean of the
observed data). In contrast, values of m either
above or below the best value lead to estimates of k
that are lower than the MLE.
Exercise 1:
Redraw the contour plot of the likelihood surface
for this data set with the contours corresponding
to a levels, as above. Add points corresponding to the
location of the MLE, the method-of-moments estimate, and the true values.
State your conclusions about the differences among these
3 sets of parameters and their statistical significance.
2 Univariate profiles
Now we'd like to find the univariate confidence limits on m and k.
It's easy enough to get an approximate idea of this graphically.
For example, for m, plotting the profile and
superimposing horizontal lines for the minimum NLL and the 95% and 99%
LRT cutoffs:
> plot(muvec, mu.profile[, "NLL"], type = "l", xlab = expression(mu),
+ ylab = "Negative log-likelihood")
> cutoffs = c(0, qchisq(c(0.95, 0.99), 1)/2)
> nll.levels = O1$value + cutoffs
> abline(h = nll.levels, lty = 1:3)
> text(rep(0.5, 3), nll.levels + 0.2, c("min", "95%", "99%"))
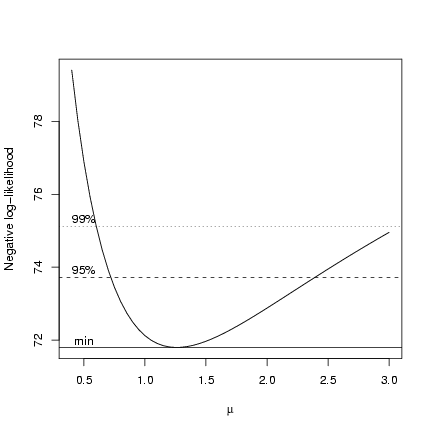But how do we find the x-intercepts (m values) associated
with the points where the likelihood profile crosses the cutoff lines?
Three possibilities:
- If we have sampled the profile at a fairly fine scale,
we can just look for the point(s) that are closest to
the cutoff value:
> cutoff = O1$value + qchisq(0.95, 1)/2
The which.min function gives the
index of the smallest element in the vector:
if we find the index corresponding to
the smallest value of the absolute
value of the profile negative log-likelihood
minus the cutoff, that should give us
the m value closest to the confidence
limit.
We actually need to to do this for each half of the curve separately.
First the lower half, selecting values from
muvec and mu.profile corresponding
to values less than 1.2 (based on looking at
the plot.
> lowerhalf = mu.profile[muvec < 1.2, "NLL"]
> lowerhalf.mu = muvec[muvec < 1.2]
> w.lower = which.min(abs(lowerhalf - cutoff))
The same thing for the upper half of the curve:
> upperhalf = mu.profile[muvec > 1.2, "NLL"]
> upperhalf.mu = muvec[muvec > 1.2]
> w.upper = which.min(abs(upperhalf - cutoff))
> ci.crude = c(lowerhalf.mu[w.lower], upperhalf.mu[w.upper])
Plot it:
> plot(muvec, mu.profile[, "NLL"], type = "l", xlab = expression(mu),
+ ylab = "Negative log-likelihood")
> cutoffs = c(0, qchisq(c(0.95), 1)/2)
> nll.levels = O1$value + cutoffs
> abline(h = nll.levels, lty = 1:2)
> abline(v = ci.crude, lty = 3)
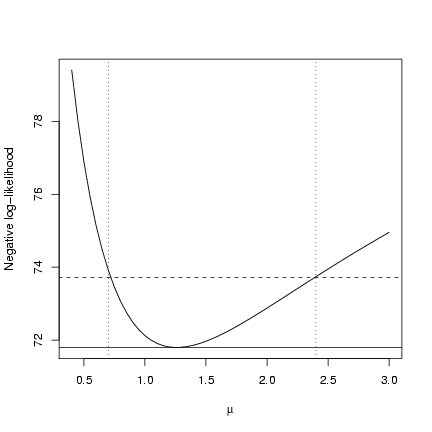You can see that it's not exactly on target,
but very close. If you wanted to proceed in this
way and needed a more precise answer you could
"zoom in" and evaluate the profile on a finer
grid around the lower and upper confidence limits.
-
You can set up an automatic search routine in R to
try to find the confidence limits.
First, define a function that takes a particular
value of m, optimizes with respect to k,
and returns the value of the negative log-likelihood
minus the cutoff value, which tells us how
far above or below the cutoff we are.
> cutoff = O1$value + qchisq(c(0.95), 1)/2
> relheight = function(mu) {
+ O2 = optim(fn = NLLfun.mu, par = O1$par["k"], method = "L-BFGS-B",
+ lower = 0.002, mu = mu)
+ O2$value - cutoff
+ }
We know the lower limit is somewhere around 0.7, so going
on either side should give us values that are
negative/positive.
> relheight(mu = 0.6)
[1] 1.420474
> relheight(mu = 0.8)
[1] -0.6530479
Using R's uniroot function, which takes
a single-parameter function and searches for a value
that gives zero:
> lower = uniroot(relheight, interval = c(0.5, 1))$root
> upper = uniroot(relheight, interval = c(1.2, 5))$root
> ci.uniroot = c(lower, upper)
> plot(muvec, mu.profile[, "NLL"], type = "l", xlab = expression(mu),
+ ylab = "Negative log-likelihood")
> cutoffs = c(0, qchisq(c(0.95), 1)/2)
> nll.levels = O1$value + cutoffs
> abline(h = nll.levels, lty = 1:2)
> abline(v = ci.crude, lty = 3)
> abline(v = ci.uniroot, lty = 4)
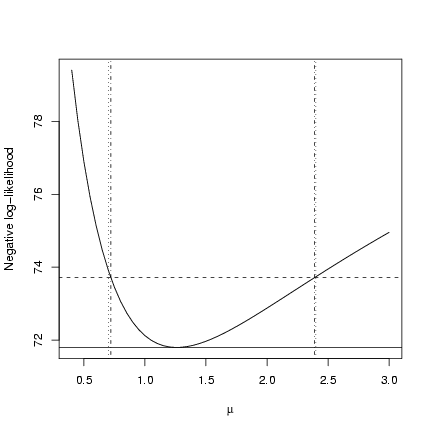Slightly more precise than the previous solution.
-
Using the information-based approach.
Here is
the information matrix:
> O1$hessian
mu k
mu 7.387808331 0.004901569
k 0.004901569 97.372581408
Inverting the information matrix:
> s1 = solve(O1$hessian)
> s1
mu k
mu 1.353581e-01 -6.813697e-06
k -6.813697e-06 1.026983e-02
You can see that the off diagonal elements
are very small (-6 ×10-6 as opposed
to 0.0102 and 0.135 on the diagonal), correctly
suggesting that the parameter estimates are
uncorrelated.
Suppose we want to approximate
the likelihood profile by the quadratic L=a+c(m-b)2.
The parameter b governs the m value at
which the minimum occurs (so b corresponds
to the MLE of m) and parameter a
governs the height of the minimum
(so a is the minimum negative log-likelihood).
The second derivative of the quadratic
is 2c; the second derivative of
the likelihood surface is
¶2 L/¶m2,
so c=(¶2 L/¶m2)/2.
> a = O1$value
> b = O1$par["mu"]
> c = O1$hessian["mu", "mu"]/2
We get the variances of the
parameters
(s2m, s2k)
by inverting
the information matrix.
The size of the confidence limit
is ±1.96 sm for 95%
confidence limits, or more generally
± qnorm(1-alpha/2) sm (qnorm
gives the quantile of the standard normal,
with mean 0 and standard deviation 1, by
default).
> se.mu = sqrt(s1["mu", "mu"])
> ci.info = O1$par["mu"] + c(-1, 1) * qnorm(0.975) * se.mu
Double plot, showing a close-up of the negative
log-likelihood minimum (to convince you that
the quadratic approximation really is a good
fit if you go close enough to the minimum - this
is essentially a Taylor expansion, provided
that the likelihood surface is reasonably well-behaved)
and a wider view comparing the quadratic
approximation and the confidence limits based on
> op = par(mfrow = c(1, 2))
> plot(muvec, mu.profile[, "NLL"], type = "l", xlab = expression(mu),
+ ylab = "Negative log-likelihood", ylim = c(71.8, 72.2), xlim = c(0.7,
+ 1.7))
> curve(a + c * (x - b)^2, add = TRUE, lty = 2)
> plot(muvec, mu.profile[, "NLL"], type = "l", xlab = expression(mu),
+ ylab = "Negative log-likelihood")
> cutoffs = c(0, qchisq(c(0.95), 1)/2) + O1$value
> curve(a + c * (x - b)^2, add = TRUE, lty = 2)
> abline(h = cutoffs)
> abline(v = ci.info, lty = 3)
> abline(v = ci.uniroot, lty = 1)
> par(op)
-
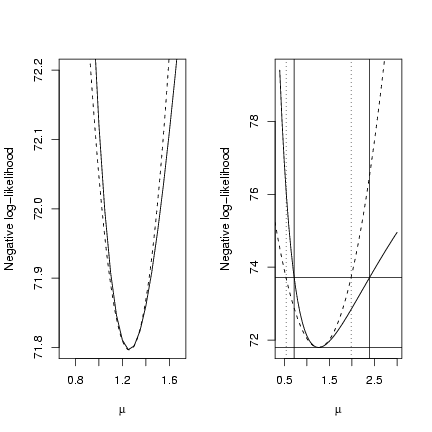
One way to cheat: use the fitdistr function
from the MASS package instead (this only
works for simple draws from distributions).
> library(MASS)
> f = fitdistr(x, "negative binomial")
> f
size mu
0.2885187 1.2597788
(0.1013610) (0.3676483)
fitdistr gives the parameters
in the other order - size and mu
rather than mu and k as I have been
naming them.
It gives standard errors based on
the quadratic approximation, so the same as by
the previous method. (I had to use str(f)
to look inside f and figure out how
to extract the numbers I wanted.)
> ci.fitdistr = f$estimate["mu"] + c(-1, 1) * f$sd["mu"] * qnorm(0.975)
- The last option is to use the mle function
from the stats4 package to find the confidence intervals.
To do this, we have to rewrite the NLL function slightly
differently: (1) specify the parameters separately, rather
than packing them into a parameter vector (and then unpacking
them inside the function - so this is actually slightly
more convenient), and (2) you can't pass the data as additional
argument: if you want to run the function for another set of
data you have to replace x with your new data, or write
another function (there are other kinds of black magic
you can do to achieve the same goal, but they are too complicated
to lay out here (P2C2E [1])).
> NLLfun2 = function(mu, k) {
+ -sum(dnbinom(x, mu = mu, size = k, log = TRUE))
+ }
mle has slightly different argument names from optim,
but you still have to specify the function and the starting values,
and you can include other options (which get passed straight
to optim):
> library(stats4)
> m1 = mle(minuslogl = NLLfun2, start = list(mu = mu.mom, k = k.mom),
+ method = "L-BFGS-B", lower = 0.002)
> m1
Call:
mle(minuslogl = NLLfun2, start = list(mu = mu.mom, k = k.mom),
method = "L-BFGS-B", lower = 0.002)
Coefficients:
mu k
1.2600009 0.2885231
summary(m1) gives the estimates and the standard errors
based on the quadratic approximation:
> summary(m1)
Maximum likelihood estimation
Call:
mle(minuslogl = NLLfun2, start = list(mu = mu.mom, k = k.mom),
method = "L-BFGS-B", lower = 0.002)
Coefficients:
Estimate Std. Error
mu 1.2600009 0.3677636
k 0.2885231 0.1013633
-2 log L: 143.5929
confint(m1) gives the profile confidence limits,
for all parameters (the second line below takes just the
row corresponding to mu).
> ci.mle.all = confint(m1)
Profiling...
> ci.mle.all
2.5 % 97.5 %
mu 0.7204352 2.390998
k 0.1437419 0.579509
> ci.mle = ci.mle.all["mu", ]
The confint code is based on first calculating the
profile (as we did above, but at a smaller number
of points), then using spline-based interpolation
to find the intersections with the cutoff height.
Comparing all of these methods:
> citab = rbind(ci.crude, ci.uniroot, ci.mle, ci.info, ci.fitdistr)
> citab
2.5 % 97.5 %
ci.crude 0.7000000 2.400000
ci.uniroot 0.7200252 2.390702
ci.mle 0.7204352 2.390998
ci.info 0.5391442 1.981327
ci.fitdistr 0.5392013 1.980356
3 Reef fish: settler distribution
Let's simulate the reef fish data again:
> a = 0.696
> b = 9.79
> recrprob = function(x, a = 0.696, b = 9.79) a/(1 + (a/b) * x)
> scoefs = c(mu = 25.32, k = 0.932, zprob = 0.123)
> settlers = rzinbinom(603, mu = scoefs["mu"], size = scoefs["k"],
+ zprob = scoefs["zprob"])
> recr = rbinom(603, prob = recrprob(settlers), size = settlers)
Set up likelihood functions - let's say we know the numbers of
settlers and are trying to estimate the recruitment probability function.
I'll use mle.
First, a Shepherd function:
> NLLfun3 = function(a, b, d) {
+ recrprob = a/(1 + (a/b) * settlers^d)
+ -sum(dbinom(recr, prob = recrprob, size = settlers, log = TRUE),
+ na.rm = TRUE)
+ }
> NLLfun4 = function(a, b) {
+ recrprob = a/(1 + (a/b) * settlers)
+ -sum(dbinom(recr, prob = recrprob, size = settlers, log = TRUE),
+ na.rm = TRUE)
+ }
> NLLfun5 = function(a) {
+ recrprob = a
+ -sum(dbinom(recr, prob = recrprob, size = settlers, log = TRUE),
+ na.rm = TRUE)
+ }
I ran into a problem with this log-likelihood function:
when settlers=0, the recruitment probability is a,
which may be greater than 0. This doesn't matter in
reality because when there are zero settlers there
aren't any recruits. From a statistical point of
view, the probability of zero recruits is 1 when
there are zero settlers, but dbinom(x,prob=a,size=0)
still comes out with NaN. However, since I
know what the problem is and I know that the
log-likelihood in this case is log(1)=0 and
so contributes nothing to the log-likelihood,
I am safe using the na.rm=TRUE option
for sum.
However, this does still gives me warnings about
NaNs produced in: dbinom ... . A better
solution might be to drop the zero-settler cases
from the data entirely:
> recr = recr[settlers > 0]
> settlers = settlers[settlers > 0]
> plot(settlers, recr)
> abline(h = 10)
> abline(a = 0, b = 0.5)
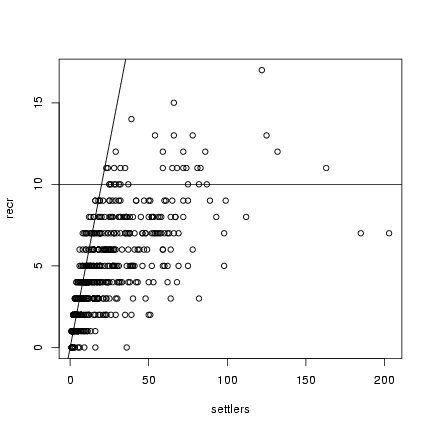Looking at a plot of the data, I can eyeball the asymptote (b) at about 10 recruits, the initial
slope (a) at about 0.5, and I'll start with d=1.
Had to mess around a bit - fitted the simpler (Beverton-Holt) model
first, and found I had to use L-BFGS-B to get mle
not to choke while computing the information matrix.
> m4 = mle(minuslogl = NLLfun4, start = list(a = 0.5, b = 10),
+ method = "L-BFGS-B", lower = 0.003)
> s3 = list(a = 0.684, b = 10.161, d = 1)
> m3 = mle(minuslogl = NLLfun3, start = s3, method = "L-BFGS-B",
+ lower = 0.003)
> m5 = mle(minuslogl = NLLfun5, start = list(a = 0.5), method = "L-BFGS-B",
+ lower = 0.003)
Plot all fits against the data:
> plot(settlers, recr)
> a = coef(m5)["a"]
> curve(a * x, add = TRUE, lty = 3)
> a = coef(m4)["a"]
> b = coef(m4)["b"]
> curve(a * x/(1 + (a/b) * x), add = TRUE, lty = 2)
> a = coef(m5)["a"]
> b = coef(m5)["b"]
> d = coef(m5)["d"]
> curve(a * x/(1 + (a/b) * x^d), add = TRUE, lty = 3)
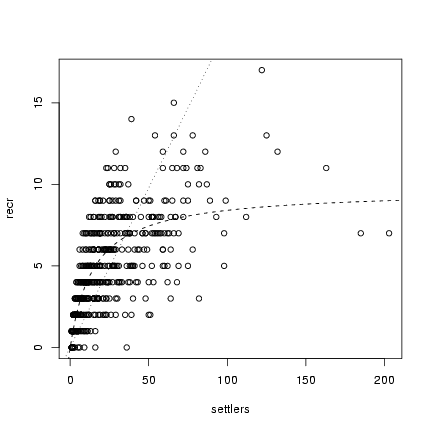Compare the negative log-likelihoods:
> nll = c(shep = -logLik(m3), BH = -logLik(m4), densind = -logLik(m5))
> nll
shep BH densind
1020.427 1020.843 1444.717
As required, the Shepherd has a better likelihood than
the Beverton-Holt, but only by a tiny amount - certainly
not greater than the LRT cutoff. On the other hand,
there is extremely strong support for density-dependence,
from the 424 log-likelihood-unit
differences between the density-independent and Beverton-Holt
model likelihoods. It's silly, but you can calculate
the logarithm of the p-value as:
> logp = pchisq(2 * nll[3] - nll[2], 1, lower.tail = FALSE, log.p = TRUE)
> logp
densind
-938.288
That's equivalent to p » 10-407.36822402525
(there's a much higher probability that the CIA broke into
your computer and tampered with your data).
We would get the same answer by calculating AIC values:
> npar = c(5, 4, 3)
> aic = nll + 2 * npar
> aic
shep BH densind
1030.427 1028.843 1450.717
Or BIC values:
> ndata = length(recr)
> bic = nll + log(ndata) * npar
> bic
shep BH densind
1051.609 1045.788 1463.426
(except that BIC says more strongly that
the Shepherd is not worth considering in this case).
The confidence intervals tell the same story:
> confint(m3)
Profiling...
2.5 % 97.5 %
a 0.5804655 0.8629449
b 4.5161010 13.2424549
d 0.8183632 1.0738295
the 95% confidence intervals of d include 1 (just).
> confint(m4)
Profiling...
2.5 % 97.5 %
a 0.5833164 0.7180549
b 8.9412876 10.4844295
We get tighter bounds on a with the Beverton-Holt
model (since we are not wasting data trying to
estimate d), and we get reasonable bounds on
b. (When I used BFGS instead of
L-BFGS-B, even though I got reasonable
answers for the MLE, I ran into trouble
when I tried to get profile confidence limits.)
In particular, the upper confidence interval
of b is < ¥ (which it would not be
if the density-independent model were a better
fit).
Exercise 2:
redo the fitting exercise, but instead of
using L-BFGS-B, fit log a,
log b, and log d to avoid having
to use constrained optimization.
Back-transform your answers
for the point estimates and the
confidence limits by exponentiating;
make sure they check closely with
the answers above.
Exercise 3:
fit zero-inflated negative binomial,
negative binomial, and Poisson distributions
to the settler data. State how the
three models are nested; perform
model selection by AIC and LRT, and
compare the confidence intervals
of the parameters.
What happens if you simulate half
as much "data"?
References
- [1]
-
Salman Rushdie.
Haroun and the Sea of Stories.
Faber & Faber, 1999.
File translated from
TEX
by
TTH,
version 3.67.
On 20 Oct 2005, 02:11.