|
|
Nicholas
Kevlahan Professor
of Mathematics
Department
of
Mathematics and Statistics |
|
|
Nicholas
Kevlahan Professor
of Mathematics
Department
of
Mathematics and Statistics |
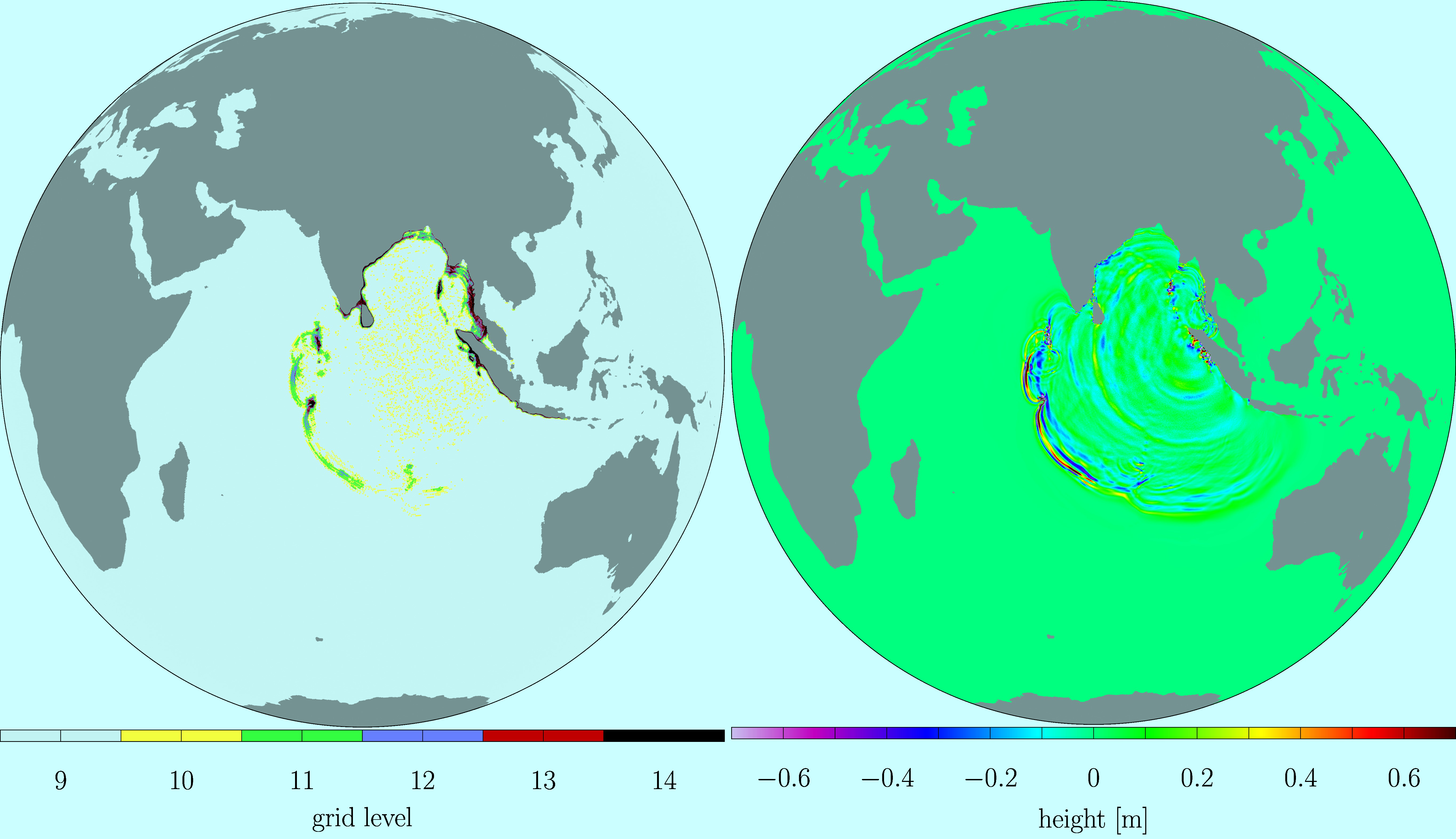 Adaptive wavelet simulation of 2004 Indian Ocean tsunami |
My research has been primarily on the theory and computation of fluid turbulence, with a special interest in numerical methods based on the wavelet transform.
There are numerous problems that
remain unresolved in the theory of turbulence, despite more than
100 years of research on the subject. A complete and precise
theory of turbulence would be useful in areas as diverse as
aerodynamics, combustion, urban pollution modelling, weather
prediction and climate modelling. Although we are still far
from being able to formulate such a theory, much progress
has been made in the last few decades. The aim of my
research is to combine several recent discoveries in order
to develop a new approach to turbulence modelling. These
discoveries include wavelet transforms (which are used to
compress data and solve partial differential equations),
penalisation methods (which can be used with any numerical
method to simulate complex geometries, such as an airplane), and
coherent vortices (flow structures that control turbulence
dynamics). The general theme of this work has been the interaction
between coherent structures (such as vortices or shocks) and the
random background in turbulence. This new approach should
allow high Reynolds number (high speed, large size) flows to be
calculated in realistic engineering or geophysical configurations.
CMLA, Ecole Normale
Superieure de Cachan, France
LMD, Ecole Normale Superieure,
Paris, France
DAMTP, University of
Cambridge, United Kingdom
Physics, University of British
Columbia, Canada
email: kevlahan@mcmaster.ca
office: Hamilton Hall - HH324