Macdonald, P.D.M. and T.J. Pitcher (1979). Age-groups from size-frequency data: a versatile and efficient method of analysing distribution mixtures. Journal of the Fisheries Research Board of Canada 36, 987-1001.
Macdonald, P.D.M. (1987). Analysis of length-frequency distributions. In R.C. Summerfelt and G.E. Hall [editors], Age and Growth of Fish, Iowa State University Press, Ames, Iowa. pp 371-384.
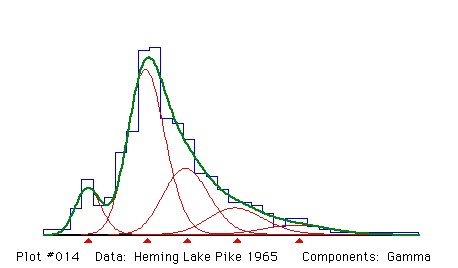
The data give the lengths of 523 pike (Esox lucius), sampled in 1965 from Heming Lake, Manitoba, Canada. There are known to be five age-groups in the sample.
Click here to see the original data: lengths to the nearest half-cm, grouped data, given as a mixed sample and as separate samples for each age group determined by scale reading.
The data are fitted by five gamma distributions with constant coefficient of variation.
The components are heavily overlapped and cannot be fitted from the mixed data alone without constraining the parameters in some way. Constant coefficient of variation is a biologically reasonable constraint for this population.

Fitting Gamma components
Proportions and their standard errors
.09684 .49464 .24084 .11729 .05039
.01477 .09961 .06781 .05954 .03311
Means and their standard errors
22.9483 33.3271 40.4566 49.2933 60.3671
.4424 .8025 2.9075 4.3763 3.4292
Sigmas (CONSTANT COEF. OF VAR. = .0993) and standard error
2.2777 3.3079 4.0155 4.8926 5.9917
.2297
Degrees of freedom = 25 - 1 + 0 - 0 - 10 - 0 = 14
Chi-squared = 11.7257 (P = .6283)
The mixed data have been supplemented by the following subsampling
data. Three fish in the size range 33.75 cm to 35.75 cm were aged and
all three were found to be from age-group 2; five fish in the size
range 35.75 cm to 37.75 cm were aged, three were found to be from
age-group 2 and two were from age-group 3; etc.
INTVL RGT BND SUM SUBSAMPLING DATA... Heming Lake Pike 1965 1 19.750 0 2 21.750 0 3 23.750 0 4 25.750 0 5 27.750 0 6 29.750 0 7 31.750 0 8 33.750 0 9 35.750 3 0 3 0 0 0 10 37.750 5 0 3 2 0 0 11 39.750 0 12 41.750 0 13 43.750 7 0 0 7 0 0 14 45.750 6 0 0 4 2 0 15 47.750 0 16 49.750 0 17 51.750 0 18 53.750 0 19 55.750 0 20 57.750 0 21 59.750 0 22 61.750 4 0 0 0 1 3 23 63.750 3 0 0 0 1 2 24 65.750 2 0 0 0 1 1 25 0
With the extra information provided by the subsampling data, there is no problem fitting all the parameters of the mixed distribution, without the need for constraints. Note that normal, lognormal and gamma distributions all fit these data equally well.

Fitting Gamma components
Proportions and their standard errors
.09856 .48379 .26991 .11410 .03364
.01815 .06149 .06738 .03743 .02185
Means and their standard errors
23.0075 33.2210 40.8063 51.1718 61.8852
.6122 .4183 1.0436 1.4953 4.7820
Sigmas and their standard errors
2.2952 3.1821 4.1105 5.4059 5.7198
.4834 .3473 .9976 1.0565 3.3099
Degrees of freedom = 25 - 1 + 35 - 7 - 14 - 11 = 27
Chi-squared = 17.5757 (P = .9160)
* WARNING * GOODNESS-OF-FIT TEST MAY BE INVALID; 14 EXPECTED COUNTS ARE < 1