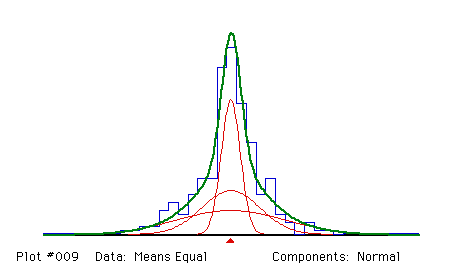
A total of 249 observations were generated by computer to follow the mixture distribution
1/3 N(12.5, 1) + 1/3 N(12.5, 3) + 1/3 N(12.5, 5)
where N(m
,s
) denotes a normal distribution with mean m
and standard deviation s
.
Fit a mixture of three normal distributions with means constrained to be equal and proportions constrained to be equal.
As with the mixture of exponential distributions, unimodality and overlap are a problem with scale mixtures. Knowing that the true proportions were equal, and so constraining the fitted proportions to be equal, helps in this example.

Fitting Normal components
Proportions and their standard errors
.33333 .33333 .33333
FIXED FIXED FIXED
Means (EQUAL) and standard error
12.4137 12.4137 12.4137
.1466
Sigmas and their standard errors
.9787 3.0073 5.5181
.1646 .5079 .5080
Degrees of freedom = 25 - 1 + 0 - 0 - 4 - 0 = 20
Chi-squared = 20.7126 (P = .4142)
This is like Analysis 1, but the proportions are also fitted.
The estimates of the proportions and standard deviations are not very good; they have very large standard errors. The estimate of the common mean is, of course, excellent, since it is well defined on the histogram.
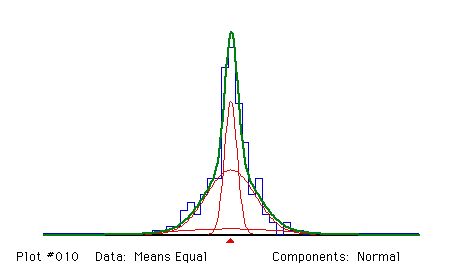
Fitting Normal components
Proportions and their standard errors
.31122 .58136 .10742
.10059 .18524 .21615
Means (EQUAL) and standard error
12.3871 12.3871 12.3871
.1466
Sigmas and their standard errors
.9228 3.5607 7.8133
.2512 .9424 5.6334
Degrees of freedom = 25 - 1 + 0 - 0 - 6 - 0 = 18
Chi-squared = 19.8656 (P = .3404)
* WARNING * GOODNESS-OF-FIT TEST MAY BE INVALID; 4 EXPECTED COUNTS ARE < 1