I have illustrated the continuity correction for the binomial distribution here, but exactly the same considerations apply when approximating any discrete distribution by a continuous distribution.
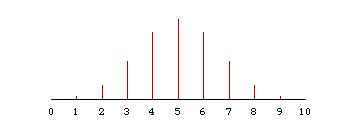
The binomial distribution is a discrete distribution. That is, a binomial random variable takes integer values. All the probability in the binomial distribution sits in discrete lumps at the integers 0, 1, ..., n.

Look at the Bin(10, 0.5) distribution. The mean is 5 and the variance is 2.5. How well does a N(5, 2.5) distribution approximate the Bin(10, 0.5)?
The normal is a continuous distribution so we have to approximate the lumps of probability at the integers by areas under the normal curve. Take P(X = 3), for example. The exact binomial probability is 0.1172.
If we integrate the N(5, 2.5) density from 2 to 3 it is too low everywhere and the result is too small.
F((3-5)/sqrt(2.5)) - F((2-5)/sqrt(2.5)) = F(-1.265) - F(-1.897) = 0.1030 - 0.0289 = 0.0741
If we integrate the N(5, 2.5) density from 3 to 4 it is too high everywhere and the result is too large.
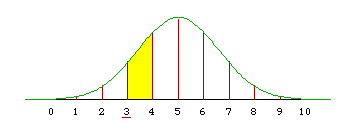
F((4-5)/sqrt(2.5)) - F((3-5)/sqrt(2.5)) = F(-0.6325) - F(-1.265) = 0.2635 - 0.1030 = 0.1605
But if we integrate from 2.5 to 3.5 the result is an much closer approximation.
F((3.5-5)/sqrt(2.5)) - F((2.5-5)/sqrt(2.5)) = F(-0.9487) - F(-1.581) = 0.1714 - 0.0569 = 0.1145
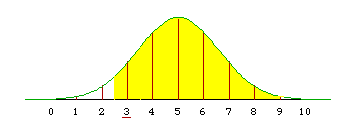
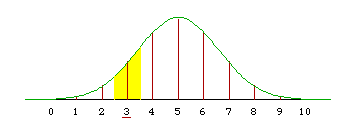
More generally, if we want to approximate the binomial probability P(X <= a), we integrate under the normal density from minus infinity to a+0.5. In the example below, a = 3 and the exact binomial calculation gives 0.1719. The normal approximation (with continuity correction) is
F((3.5-5)/sqrt(2.5)) = F(-0.9487) = 0.1714
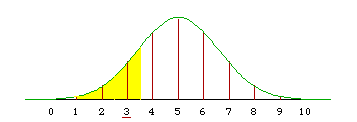
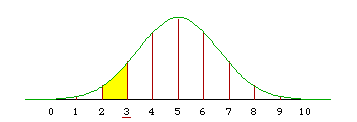
If we want to approximate the binomial probability that P(X >= a), we integrate the normal density from a-0.5 to infinity. In the example below, a = 3 and the exact binomial calculation gives 0.9453. The normal approximation (with continuity correction) is
1 - F((2.5-5)/sqrt(2.5)) = 1 - F(-1.581) = 1 - 0.0569 = 0.9431.