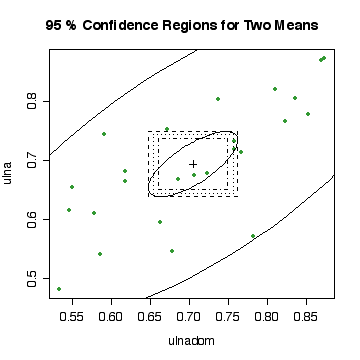
The function confp() computes the 100(1 - alpha)%
confidence ellipsoid for a multivariate normal mean, and confidence
boxes by the univariate, Bonferroni and shadow methods. The
univariate method gives the smallest box, the shadow method gives the
largest box, just enclosing the ellipsoid.
When the data are bivariate, the ellipse and rectangles are
plotted. If plotdata = T, the original data appear on a
scatterplot and a concentration ellipse (at the same alpha as the
confidence ellipse) is drawn.
> confp <-
function (x, plotdata = F, alpha = 0.05, ...)
{
n <- nrow(x)
p <- ncol(x)
if (p >= 2) {
crite <- ((p * (n - 1))/(n * (n - p))) * qf(1 - alpha,
p, n - p)
critm <- qt(1 - (alpha/2), n - 1)/sqrt(n)
critb <- qt(1 - (alpha/(2 * p)), n - 1)/sqrt(n)
smat <- var(x)
mean <- apply(x, 2, mean)
x.ei <- eigen(smat)
hlaxe <- sqrt(x.ei$values * crite)
theta <- angle(x.ei$vectors[1, 1], x.ei$vectors[2, 1])
hlbx <- sqrt(diag(smat) * crite)
hlbxm <- sqrt(diag(smat)) * critm
hlbxb <- sqrt(diag(smat)) * critb
if (p == 2) {
if (plotdata) {
plot(x[, 1], x[, 2], xlab = dimnames(x)[[2]][1],
ylab = dimnames(x)[[2]][2], ...)
ellipse(sqrt(n) * hlaxe[1], sqrt(n) * hlaxe[2],
theta, mean[1], mean[2])
}
else plot(c(mean[1] - hlbx[1], mean[1] + hlbx[1]),
c(mean[2] - hlbx[2], mean[2] + hlbx[2]), xlab = dimnames(x)[[2]][1],
ylab = dimnames(x)[[2]][2], type = "n")
points(mean[1], mean[2], pch = 3)
title(main = paste(100 * (1 - alpha), "% Confidence Regions for Two Means"))
rect(mean[1] - hlbx[1], mean[2] - hlbx[2], mean[1] +
hlbx[1], mean[2] + hlbx[2], lty = 2)
rect(mean[1] - hlbxm[1], mean[2] - hlbxm[2], mean[1] +
hlbxm[1], mean[2] + hlbxm[2], lty = 4)
rect(mean[1] - hlbxb[1], mean[2] - hlbxb[2], mean[1] +
hlbxb[1], mean[2] + hlbxb[2], lty = 3)
ellipse(hlaxe[1], hlaxe[2], theta, mean[1], mean[2])
}
list(mean = mean, smat = smat, hlaxe = hlaxe, axes = x.ei$vectors,
theta = theta, hlbx = hlbx, hlbxm = hlbxm, hlbxb = hlbxb)
}
}
> confp(bones[,5:6], T, pch=19, col="forestgreen")
$mean
ulnadom ulna
0.70440 0.69384
$smat
ulnadom ulna
ulnadom 0.01156842 0.00807115
ulna 0.00807115 0.01059914
$hlaxe
[1] 0.07400143 0.02926561
$axes
[,1] [,2]
[1,] 0.7279896 0.6855881
[2,] 0.6855881 -0.7279896
$theta
[1] 0.7554113
$hlbx
ulnadom ulna
0.05748732 0.05502631
$hlbxm
ulnadom ulna
0.04439717 0.04249655
$hlbxb
ulnadom ulna
0.05143246 0.04923066
>
