Contents
function out = ponzi()
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % This code simulates the Keen model with Ponzi financing % as specified in Grasselli and Costa Lima (2012) % % % authors: B. Costa Lima and M. Grasselli %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% close all clc warning off
Parameters attribution
Equations (24), (26), (63), (65) and (90)
nu = 3; % capital-to-output ratio alpha = 0.025; % productivity growth rate beta = 0.02; % population growth rate delta = 0.01; % depreciation rate phi0 = 0.04/(1-0.04^2); %Phillips curve parameter, Phi(0.96)=0 phi1 = 0.04^3/(1-0.04^2); %Phillips curve parameter, Phi(0)=-0.04 r = 0.03; %real interest rate kappa0 = -0.0065 ; % investment function parameter kappa1 = exp(-5); % investment function parameter kappa2 = 20; % investment function parameter psi0 =-0.25; % speculation function parameter psi1 =0.25*exp(-0.36); % speculation function parameter psi2 =12;
Other definitions
TOL = 1E-7; options = odeset('RelTol', TOL); txt_format = '%3.3g';
Functions Definition
fun_Phi = @(x) phi1./(1-x).^2- phi0; % Phillips curve, equation (25) fun_Phi_prime = @(x) 2*phi1./(1-x).^3; % derivative of Phillips curve fun_Phi_inv = @(x) 1 - (phi1/(x+phi0)).^(1/2); % inverse of Phillips curve fun_kappa = @(x) kappa0+kappa1.*exp(kappa2.*x); % Investment function, equation (64) fun_kappa_prime = @(x) kappa1.*kappa2.*exp(kappa2.*x); % Derivative of investment function fun_kappa_inv = @(x) log((x-kappa0)./kappa1)./kappa2; % Inverse of investment function fun_Psi = @(x) psi0+psi1.*exp(psi2.*x); % speculation function, equation (89)
Sample paths of the Keen model with speculation
bar_pi_n_K = fun_kappa_inv(nu*(alpha+beta+delta)); bar_d_K = (fun_kappa(bar_pi_n_K)-bar_pi_n_K)/(alpha+beta); bar_omega_K = 1-bar_pi_n_K-r*bar_d_K; bar_lambda_K = fun_Phi_inv(alpha); omega0 = 0.95; lambda0 = 0.9; d0 = 0; p0 =0.1; Y0 = 100; T = 200; [tK,yK] = ode15s(@(t,y) keen(y), [0 T], convert([omega0, lambda0, d0]), options); yK = retrieve(yK); Y_output = Y0*yK(:,2)/lambda0.*exp((alpha+beta)*tK); [tP,yP] = ode15s(@(t,y) ponzi(y), [0 T], convert([omega0, lambda0, d0, p0]), options); yP = retrieve(yP); Y_output_ponzi = Y0*yP(:,2)/lambda0.*exp((alpha+beta)*tP); % Figure 7 figure(1) plot(yK(:,2), yK(:,1),'-k'), hold on; plot(yP(:,2), yP(:,1),'--b') xlabel('\lambda') ylabel('\omega') title(['\omega_0 = ', num2str(omega0, txt_format), ... ', \lambda_0 = ', num2str(lambda0, txt_format), ... ', d_0 = ', num2str(d0, txt_format), ... ', p_0 = ', num2str(p0, txt_format), ... ', Y_0 = ', num2str(Y0, txt_format)]) legend('No Speculation ', 'Ponzi Financing','Location','NorthWest') print('keen_ponzi_phase','-depsc') % Figure 8 figure(2) fig = figure; left_color = [0 0 1]; right_color = [0.5 0.7 0.2]; set(fig,'defaultAxesColorOrder',[left_color; right_color]); title(['\omega_0 = ', num2str(omega0, txt_format), ... ', \lambda_0 = ', num2str(lambda0, txt_format), ... ', d_0 = ', num2str(d0, txt_format), ... ', p_0 = ', num2str(p0, txt_format), ... ', Y_0 = ', num2str(Y0, txt_format)]) subplot(3,1,1) yyaxis right plot(tP, yP(:,3),'--','color',[0.5 0.7 0.2]') ylabel('d with Ponzi') yyaxis left plot(tK, yK(:,3),'-b') ylabel('d') legend('No Speculation ', 'Ponzi Financing','Location','NorthEast') subplot(3,1,2) yyaxis right plot(tP, Y_output_ponzi,'--','color',[0.5 0.7 0.2]') ylabel('Y with Ponzi') yyaxis left plot(tK, Y_output,'-b') ylabel('Y') legend('No Speculation ', 'Ponzi Financing','Location','NorthEast') subplot(3,1,3) plot(tP, yP(:,4),'-b') ylabel('p') print('keen_ponzi_time','-depsc')
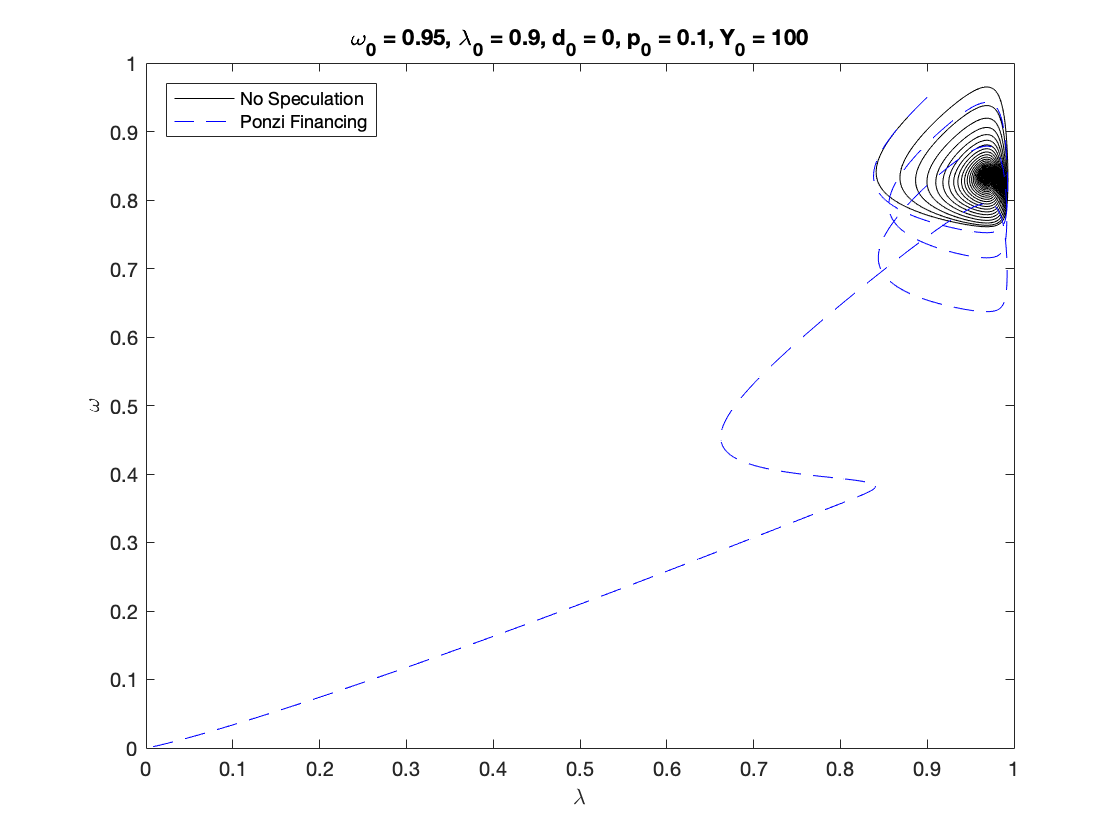

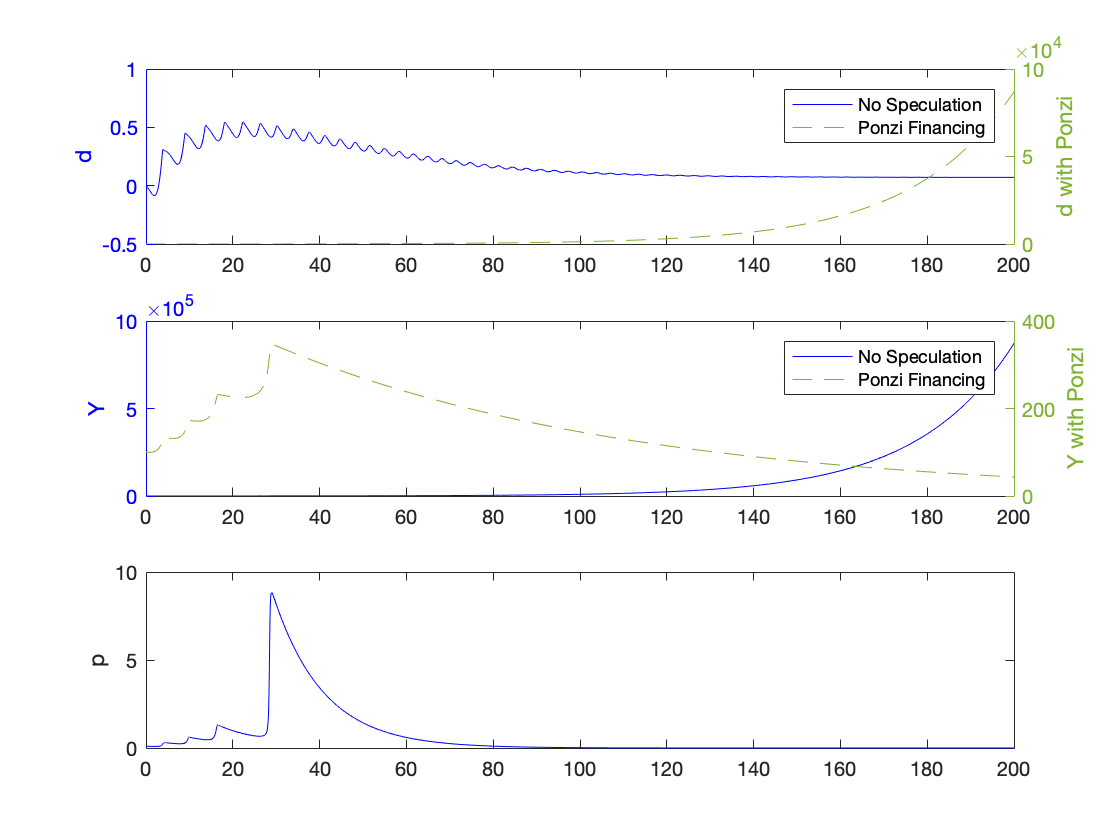
Auxiliary functions
Instead of integrating the system in terms of omega, lambda and d, we decided to use:
log_omega = log(omega), tan_lambda = tan((lambda-0.5)*pi), and pi_n=1-omega-r*d log_p = log(p)
Experiments show that the numerical methods work better with these variables.
function new = convert(old) % This function converts % [omega, lambda, d, p] % to % [log_omega, tan_lambda, pi_n, log_p] % It also work with the first 2 or 3 elements alone. % each of these variables might also be a time-dependent vector n = size(old,2); %number of variables new = zeros(size(old)); new(:,1) = log(old(:,1)); new(:,2) = tan((old(:,2)-0.5)*pi); if n>2 new(:,3) = 1-old(:,1)-r*old(:,3); if n==4 new(:,4) = log(old(:,4)); end end end function old = retrieve(new) % This function retrieves [omega, lambda, d, p] % from % [log_omega, tan_lambda, pi_n, log_p] % % It also work with the first 2 or 3 elements alone. % each of these variables might also be a time-dependent vector n = size(new,2); %number of variables old = zeros(size(new)); old(:,1) = exp(new(:,1)); old(:,2) = atan(new(:,2))/pi+0.5; if n>2 old(:,3) = (1-old(:,1)-new(:,3))/r; if n==4 old(:,4) = exp(new(:,4)); end end end function f = keen(y) f = zeros(3,1); log_omega = y(1); tan_lambda = y(2); pi_n = y(3); lambda = atan(tan_lambda)/pi+0.5; omega = exp(log_omega); g_Y = fun_kappa(pi_n)/nu-delta; % Equation (47) f(1) = fun_Phi(lambda)-alpha; %d(log_omega)/dt f(2) = (1+tan_lambda^2)*pi*lambda*(g_Y-alpha-beta); %d(tan_lambda)/dt f(3) = -omega*f(1)-r*(fun_kappa(pi_n)-pi_n)+(1-omega-pi_n)*g_Y; %d(pi_n)/dt end function f = ponzi(y) f = zeros(4,1); log_omega = y(1); tan_lambda = y(2); pi_n = y(3); log_p = y(4); lambda = atan(tan_lambda)/pi+0.5; omega = exp(log_omega); p = exp(log_p); g_Y = fun_kappa(pi_n)/nu-delta; % Equation (74) f(1) = fun_Phi(lambda)-alpha; %d(log_omega)/dt f(2) = (1+tan_lambda^2)*pi*lambda*(g_Y-alpha-beta); %d(tan_lambda)/dt f(3) = -omega*f(1)-r*(fun_kappa(pi_n)-pi_n)+(1-omega-pi_n)*g_Y-r*p; %d(pi_n)/dt f(4) = fun_Psi(g_Y) - g_Y; %dp/dt end
end