Statistics 2MA3 - Assignment #3 Solutions

2003-04-10 [Revisions to Q4b and Q7 solutions on 2003-04-14]

Full marks = 140

Q1

[MARKS: 5]

The ratio of upper limit to lower limit is just the chi-square 0.975 quantile divided by the 0.025 quantile, it does not depend on the sample variance; checking this ratio for several degrees of freedom gives 27 degrees of freedom as the answer, which means that 28 observations are needed.

> data.frame(df=20:30,ratio=qchisq(.975,20:30)/qchisq(.025,20:30))
   df    ratio
1  20 3.562757
2  21 3.450280
3  22 3.349084
4  23 3.257514
5  24 3.174228
6  25 3.098120
7  26 3.028276
8  27 2.963932
9  28 2.904442
10 29 2.849260
11 30 2.797920

Q2

[MARKS: 8 for (a), 8 for (b), 8 for (c)]

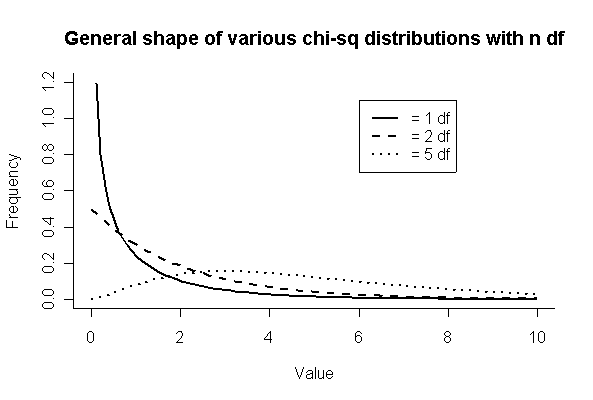
(a) Note that I gave up trying to match the tic-marks exactly.

> xgr <- seq(0,10,len=100)
> plot(xgr,dchisq(xgr,1),type="l",xlim=c(0,10),ylim=c(0,1.2),
xlab="Value",ylab="Frequency",lwd=2,bty="l")
Warning message: 
NaNs produced in: dchisq(x, df, log) 
> lines(xgr,dchisq(xgr,2),lwd=2,lty=2)
> lines(xgr,dchisq(xgr,5),lwd=2,lty=3)
> legend(6,1.1,c("= 1 df","= 2 df","= 5 df"),lwd=2,lty=1:3)
> title("General shape of various chi-sq distributions with n df")

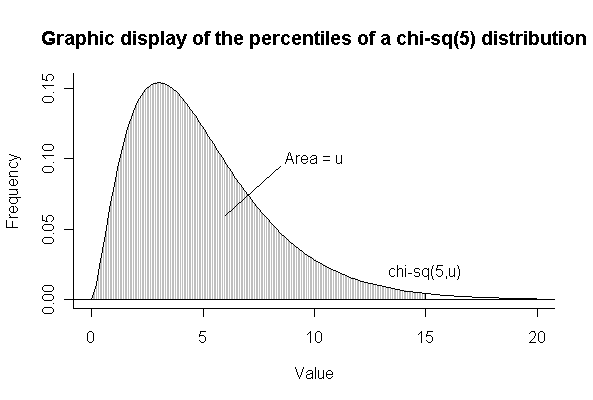
(b) Note that u = 0.9896377 from the pchisq(15,5) calculation below.

> xgr <- seq(0,20,len=100)
> xgr15 <- seq(0,15,len=200)
> plot(xgr,dchisq(xgr,5),xlab="Value",ylab="Frequency",type="l",bty="l")
> abline(h=0)
> lines(xgr15,dchisq(xgr15,5),type="h",col="gray")
> lines(15,dchisq(15,5),type="h")
> lines(xgr,dchisq(xgr,5))
> text(10,.1,"Area = u")
> lines(c(6,8.5),c(.06,.095))
> text(15,0.02,"chi-sq(5,u)")
> title("Graphic display of the percentiles of a chi-sq(5) distribution")
> pchisq(15,5)
[1] 0.9896377

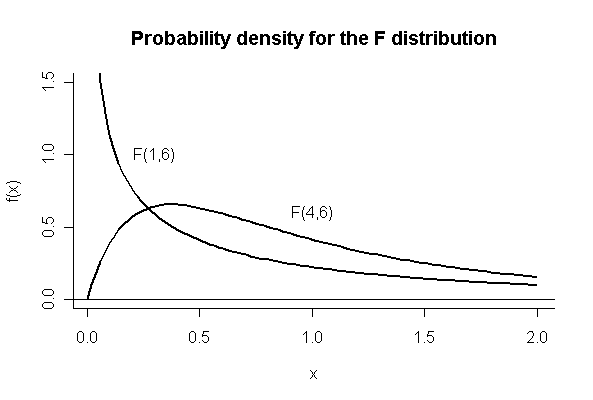
(c)

> xgr <- seq(0,2,len=100)
> plot(xgr[-1],df(xgr[-1],1,6),type="l",lwd=2,ylim=c(0,1.5),xlab="x",ylab="f(x)",bty="l")
> abline(h=0)
> lines(xgr,df(xgr,4,6),lwd=2)
> text(0.3,1,"F(1,6)")
> text(1,0.6,"F(4,6)")
> title("Probability density for the F distribution")

Q3

[MARKS: 15]

Odds ratio

> 1975*310/(1627*255)
[1] 1.47571

The odds for a boy are 47.6% higher for nonsmokers, compared to smokers.

Risk ratio

> (1975/(1975+1627))/(255/(255+310))
[1] 1.214875

The probability of having a boy is 21.5% higher for nonsmokers, compared to smokers.

> (310/(255+310))/(1627/(1975+1627))
[1] 1.214701

The probability that both parents smoke is 21.5% higher for parents of a girl, compared to parents of a boy.

Pearson's Chi-square test

> sexrat <- chisq.test(matrix(c(1975, 1627, 255, 310), ncol = 2),correct=F)
> sexrat
 
	Pearson's Chi-squared test
 
data:  matrix(c(1975, 1627, 255, 310), ncol = 2) 
X-squared = 18.4645, df = 1, p-value = 1.731e-05
 
> sexrat$obs
     [,1] [,2]
[1,] 1975  255
[2,] 1627  310
> sexrat$exp
         [,1]     [,2]
[1,] 1927.636 302.3638
[2,] 1674.364 262.6362

Assumption:

The babies are selected independently of each other.

Conclusion:

The chance of having a girl is significantly higher (P < 0.0001) for smoking parents than for nonsmoking parents.

Q4

[MARKS: 25]

(a)

> bmi1
   base twoyr
1  26.5  26.1
2  26.1  26.4
3  25.4  25.5
4  27.4  26.3
5  25.4    NA
6  25.4  25.7
7  25.8  26.1
8  26.3  26.2
9  26.5  26.5
10 26.1  26.4
11 26.4  26.2
12 25.9  26.4
13 25.5  25.6
14 25.7  24.9
15 25.4  25.9
16 27.0  26.5

Valid Analysis - Paired t-test

Graph: dot plot, box plot or histogram of the differences.
Assumptions: subjects are independent (can't test), differences are normal (not valid as the histogram is positively skewed, perhaps should look at differences on a log scale), mean difference does not depend on the base BMI (look at the scatter plot and test the hypothesis that the relationship is a straight line slope with slope equal to 1).
Conclusion: There is no evidence (P = 0.71) of a change in BMI between the base measurement and the two-year follow-up.

> t.test(bmi1$base,bmi1$twoyr,pair=T)
 
	Paired t-test
 
data:  bmi1$base and bmi1$twoyr 
t = 0.3806, df = 14, p-value = 0.7092
alternative hypothesis: true difference in means is not equal to 0 
95 percent confidence interval:
 -0.2163206  0.3096539 
sample estimates:
mean of the differences 
             0.04666667

Valid Analysis - Sign Test

Graph: dot plot, box plot or histogram of the differences.
Assumptions: subjects are independent (can't test).
Conclusion: There are 14 non-zero differences, 6 of them positive. There is no evidence (P = 0.79) of a change in BMI between the base measurement and the two-year follow-up.

> bmi1$base-bmi1$twoyr
 [1]  0.4 -0.3 -0.1  1.1   NA -0.3 -0.3  0.1  0.0 -0.3  0.2 -0.5 -0.1  0.8
[15] -0.5  0.5
> 2*pbinom(6,14,.5)
[1] 0.7905273

Valid Analysis - Simple Linear Regression

Graph: scatter plot.
Assumptions: subjects are independent (can't test).
Conclusion: There is some evidence (P = 0.012) of a positive slope, that is, subjects with a higher than average base BMI also tend to have a higher than average BMI at two-year follow-up. This is not a very interesting conclusion. It would be of interest to test the hypothesis that the slope is 1 as this would validate an assumption of the paired t-test

> anova(lm(twoyr~base,data=bmi1))
Analysis of Variance Table
 
Response: twoyr
          Df Sum Sq Mean Sq F value  Pr(>F)  
base       1 1.1218  1.1218  8.4025 0.01244 *
Residuals 13 1.7356  0.1335                  
---
Signif. codes:  0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 
> summary(lm(twoyr~base,data=bmi1))
 
Call:
lm(formula = twoyr ~ base, data = bmi1)
 
Residuals:
     Min       1Q   Median       3Q      Max 
-0.96164 -0.15276  0.02683  0.22668  0.44428 
 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)  13.7721     4.2356   3.252  0.00631 **
base          0.4704     0.1623   2.899  0.01244 * 
---
Signif. codes:  0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 
 
Residual standard error: 0.3654 on 13 degrees of freedom
Multiple R-Squared: 0.3926,	Adjusted R-squared: 0.3459 
F-statistic: 8.402 on 1 and 13 DF,  p-value: 0.01244 
 
> plot(rep(0,16),bmi1$base-bmi1$twoyr)
> boxplot(bmi1$base-bmi1$twoyr)
> title(ylab="base - twoyr")
> hist(bmi1$base-bmi1$twoyr)
> plot(bmi1$base,bmi1$twoyr)
> abline(0,1)
> abline(lm(twoyr~base,data=bmi1), lty=2)

(b)

Valid Analysis - 2-sample t-test or one-way ANOVA

Graph: comparative box plot.
Assumptions: subjects are independent (can't test), pH measurements are normal (looks OK on box plots, except for the outlier in the upstream sample), homoscedasticity (do an F-test to compare the two variances).
Conclusion: There is no evidence (P = 0.272) of a difference in mean pH between the upstream and downstream sampling locations. The assumption of homoscedasticity is rejected, however (P = 0.004), and this suggests that the analysis is not valid. This is almost entirely because of the one outlier, the third observation in the upstream sample.

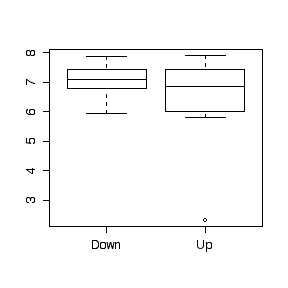
> t.test(creek$pH[creek$loc=="Up"],creek$pH[creek$loc=="Down"],var=T)

Two Sample t-test

data: creek$pH[creek$loc == "Up"] and creek$pH[creek$loc == "Down"]
t = -1.133, df = 18, p-value = 0.2721
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-1.7325194 0.5185194
sample estimates:
mean of x mean of y
    6.461     7.068

> anova(lm(pH~location,data=creek))
Analysis of Variance Table

Response: pH
          Df Sum Sq Mean Sq F value Pr(>F)
location   1 1.8422 1.8422 1.2838 0.2721
Residuals 18 25.8303 1.4350
> F0 <- var(creek$pH[creek$loc=="Up"])/var(creek$pH[creek$loc=="Down"])
> F0
[1] 8.43619
> 2*(1-pf(F0,9,9))
[1] 0.003964524
> var(creek$pH[creek$loc=="Up"])
[1] 2.565877
> var(creek$pH[creek$loc=="Down"])
[1] 0.3041511
> boxplot(split(creek$pH,creek$location))

Valid Analysis - 2-sample t-test or one-way ANOVA with outlier removed

Graph: comparative box plot.
Assumptions: subjects are independent (can't test), pH measurements are normal (looks OK on box plots), homoscedasticity (do an F-test to compare the two variances).
Conclusion: There is no evidence (P = 0.62) of a difference in mean pH between the upstream and downstream sampling locations. The assumption of homoscedasticity is accepted (P = 0.465).

> var(creek$pH[creek$loc=="Up"][-3])
[1] 0.5049611
> F0a <- var(creek$pH[creek$loc=="Up"][-3])/var(creek$pH[creek$loc=="Down"])
> F0a
[1] 1.660231
> 2*(1-pf(F0a,8,9))
[1] 0.4654831
> anova(lm(pH~location,data=creek[-3,]))
Analysis of Variance Table

Response: pH
          Df Sum Sq Mean Sq F value Pr(>F)
location   1 0.1022 0.1022 0.2564 0.6191
Residuals 17 6.7770 0.3986

Q5

[MARKS: 11]

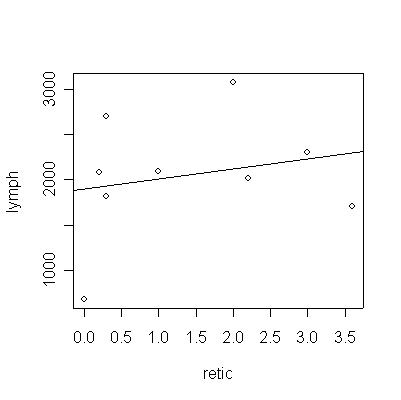
All of the required answers are found in the output below. There is, of course, no evidence (P = 0.56 by the F- test in the ANOVA or by the t-test on the slope) of a relationship between % reticulytes and lymphocytes per mm². This is confirmed by the R² which is near 0, which means that linear prediction is not possible.

The mean square residual gives s²_y.x = 490818.

> anemia
  retic lymph
1   3.6  1700
2   2.0  3078
3   0.3  1820
4   0.3  2706
5   0.2  2086
6   3.0  2299
7   0.0   676
8   1.0  2088
9   2.2  2013

> fitanemia<-lm(lymph~retic,anemia)
> plot(lymph~retic,anemia)
> abline(fitanemia)
> anova(fitanemia)
Analysis of Variance Table

Response: lymph
          Df  Sum Sq Mean Sq F value Pr(>F)
retic      1  180750  180750  0.3683 0.5631
Residuals  7 3435727  490818               
> summary(fitanemia)

Call:
lm(formula = lymph ~ retic, data = anemia)

Residuals:
     Min       1Q   Median       3Q      Max 
-1218.82  -128.47    67.84   168.76   958.95 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   1894.8      348.5   5.437 0.000969 ***
retic          112.1      184.7   0.607 0.563109    
---
Signif. codes:  0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 

Residual standard error: 700.6 on 7 degrees of freedom
Multiple R-Squared: 0.04998,    Adjusted R-squared: -0.08574 
F-statistic: 0.3683 on 1 and 7 DF,  p-value: 0.5631

Q6

[MARKS: 10]

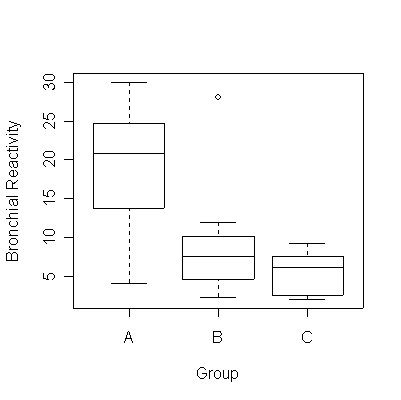
There is some evidence (P = 0.018) that the mean bronchial reactivity varies between the three groups based on the ratio FEV₁/FVC. Note that the graph suggests that Group A has greater variance than B or C but the sample sizes are too small to be sure.

> lung
   react group
1   20.8     A
2    4.1     A
3   30.0     A
4   24.7     A
5   13.8     A
6    7.5     B
7    7.5     B
8   11.9     B
9    4.5     B
10   3.1     B
11   8.0     B
12   4.7     B
13  28.1     B
14  10.3     B
15  10.0     B
16   5.1     B
17   2.2     B
18   9.2     C
19   2.0     C
20   2.5     C
21   6.1     C
22   7.5     C

> boxplot(react~group,lung,xlab="Group",ylab="Bronchial Reactivity")
> anova(lm(react~group,lung))
Analysis of Variance Table

Response: react
          Df Sum Sq Mean Sq F value  Pr(>F)  
group      2 503.55  251.77  4.9893 0.01813 *
Residuals 19 958.80   50.46                  
---
Signif. codes:  0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1

Q7

[MARKS: ANOVA 12, CI for residual variance 2, Either graph 4, Assumptions 3, Test assumptions 1, Conclusions 3]

[PART MARKS: Deduct at most 1 mark per error in computing the ANOVA table; give at most 2 marks for a less appropriate graph.]

Assumptions:

Independence, Normality, Homoscedasticity.
None of these assumptions can be tested effectively because there are only 2 replications at each design point and only 12 df for the residual.

Conclusions:

There is no evidence (P = 0.44) of an interaction between poison and antidote, so we can test the main effects, both of which are significant (P < 0.001 for poison, P = 0.004 for antidote). Hence poison and antidode both affect the mean survival time and the mean effect of each antidote is the same for each poison. The interaction plots are sufficiently parallel to give visual confirmation of no interaction.

Calculations:

> toxic1
   life poison antidote
1  0.31      I        A
2  0.46      I        A
3  0.36     II        A
4  0.40     II        A
5  0.22    III        A
6  0.18    III        A
7  0.82      I        B
8  0.88      I        B
9  0.92     II        B
10 0.49     II        B
11 0.30    III        B
12 0.38    III        B
13 0.43      I        C
14 0.63      I        C
15 0.44     II        C
16 0.31     II        C
17 0.23    III        C
18 0.24    III        C
19 0.45      I        D
20 0.66      I        D
21 0.56     II        D
22 0.71     II        D
23 0.30    III        D
24 0.31    III        D

> anova(lm(life~poison*antidote, data=toxic1))
Analysis of Variance Table

Response: life
                Df  Sum Sq Mean Sq F value    Pr(>F)    
poison           2 0.43641 0.21820 15.2103 0.0005124 ***
antidote         3 0.33875 0.11292  7.8709 0.0036184 ** 
poison:antidote  6 0.08989 0.01498  1.0443 0.4445361    
Residuals       12 0.17215 0.01435                      
---
Signif. codes:  0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 

> mse <- anova(lm(life~poison*antidote, data=toxic1))$"Mean Sq"[4]
> mse
           
0.01434583 
> mse/c(qchisq(.995,12)/12, qchisq(.005,12)/12)
[1] 0.006083142 0.056005165

Graphs:

Q8

[MARKS: ANOVA with Lack of Fit 10, Either CI for residual variance 2, Graph 3, Assumptions 3, Test assumptions 3, Conclusions and prediction 4]

[PART MARKS: Deduct at most 1 mark per error in computation.]

Assumptions:

Independence, Normality, Homoscedasticity, Linearity.
Linearity is accepted by the lack of fit test in the ANOVA. The scatter of points around the fitted line is reasonably even and symmetric, suggesting that the assumptions of normality and homoscedasticity are not unreasonable.

Conclusions:

There is no evidence (P = 0.70) from these data of nonlinearity, so we can proceed to test the slope. There is evidence (P = 0.01) that the slope is not zero, so we can conclude that WRAT is linearly related to PIAT.
If we assume linearity, the slope is highly significant (P < 0.00001).
R² = 0.93 so PIAT gives an accurate prediction of WRAT, at least within the range of scores in the data.

Calculations:

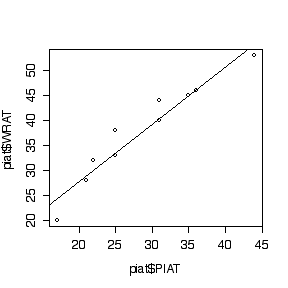
> plot(piat$PIAT,piat$WRAT)
> abline(lm(WRAT~PIAT,data=piat))
> summary(lm(WRAT~PIAT,data=piat))
 
Call:
lm(formula = WRAT ~ PIAT, data = piat)
 
Residuals:
    Min      1Q  Median      3Q     Max 
-4.4511 -0.9485 -0.4175  1.3157  4.3531 
 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   4.9099     3.3642   1.459    0.183    
PIAT          1.1495     0.1131  10.161 7.53e-06 ***
---
Signif. codes:  0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 
 
Residual standard error: 2.785 on 8 degrees of freedom
Multiple R-Squared: 0.9281,	Adjusted R-squared: 0.9191 
F-statistic: 103.2 on 1 and 8 DF,  p-value: 7.535e-06 
 
> anova(lm(WRAT~PIAT,data=piat))
Analysis of Variance Table
 
Response: WRAT
          Df Sum Sq Mean Sq F value    Pr(>F)    
PIAT       1 800.84  800.84  103.24 7.535e-06 ***
Residuals  8  62.06    7.76                      
---
Signif. codes:  0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 
> anova(lm(WRAT~PIAT+as.factor(PIAT),data=piat))
Analysis of Variance Table
 
Response: WRAT
                Df Sum Sq Mean Sq F value  Pr(>F)  
PIAT             1 800.84  800.84 78.1310 0.01256 *
as.factor(PIAT)  6  41.56    6.93  0.6757 0.69970  
Residuals        2  20.50   10.25                  
---
Signif. codes:  0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 
> mse1 <- anova(lm(WRAT~PIAT,data=piat))$"Mean Sq"[2]
> mse2 <- anova(lm(WRAT~PIAT+as.factor(PIAT),data=piat))$"Mean Sq"[3]
> mse1
         
7.757136 
> mse1/c(qchisq(.995,8)/8,qchisq(.005,8)/8)
[1]  2.826564 46.159240
> mse2
      
10.25 
> mse2/c(qchisq(.995,2)/2,qchisq(.005,2)/2)
[1]    1.934576 2044.870718
> predict(lm(WRAT~PIAT,data=piat),data.frame(PIAT=30))
[1] 39.39432

Graph: