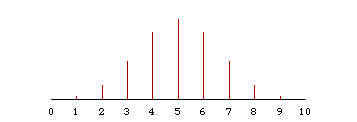
I have illustrated the continuity correction for the binomial distribution here, but exactly the same considerations apply when approximating any discrete distribution by a continuous distribution.
The binomial distribution is a discrete distribution. That is, a binomial random variable takes integer values. All the probability in the binomial distribution sits in discrete lumps at the integers 0, 1, ..., n.

Use R or the spreadsheet you wrote for Exercise 2 and look at the Bin(10, 0.5) distribution. The mean is 5 and the variance is 2.5. How does a N(5, 2.5) distribution approximate the Bin(10, 0.5)?
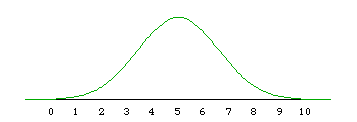
The normal is a continuous distribution so we have to approximate the lumps of probability at the integers by areas under the normal curve. Take P(X = 3), for example. The exact binomial probability is 0.1172.
If we integrate the N(5, 2.5) density from 2 to 3 it is too low everywhere and the result is too small.
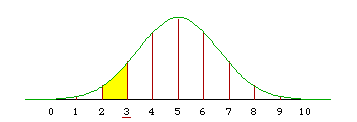
F((3-5)/sqrt(2.5)) - F((2-5)/sqrt(2.5)) = F(-1.265) - F(-1.897) = 0.1030 - 0.0289 = 0.0741
If we integrate the N(5, 2.5) density from 3 to 4 it is too high everywhere and the result is too large.
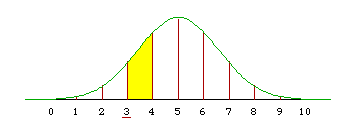
F((4-5)/sqrt(2.5)) - F((3-5)/sqrt(2.5)) = F(-0.6325) - F(-1.265) = 0.2635 - 0.1030 = 0.1605
But if we integrate from 2.5 to 3.5 the result is an much closer approximation.
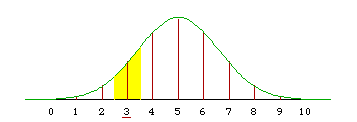
F((3.5-5)/sqrt(2.5)) - F((2.5-5)/sqrt(2.5)) = F(-0.9487) - F(-1.581) = 0.1714 - 0.0569 = 0.1145
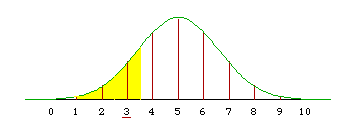
More generally, if we want to approximate the binomial probability P(X <= a), we integrate under the normal density from minus infinity to a+0.5.
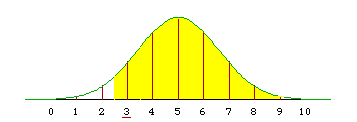
If we want to approximate the binomial probability that P(X >= a), we integrate the normal density from a-0.5 to infinity.
In the "washer and pin" problem from the 2003-02-26 lecture, the diameter of the pin shaft is assumed to follow a normal distribution, as is the diameter of the washer hole. Hence the difference between the two diameters, L, also follows a normal distribution, N(1, 2) to be exact. There is nothing discrete or integer-valued about this problem. L can take any value over a continuous range. Hence if we want P(L > 0) we integrate the N(1, 2) density from 0 to infinity. The continuity correction is not relevant.