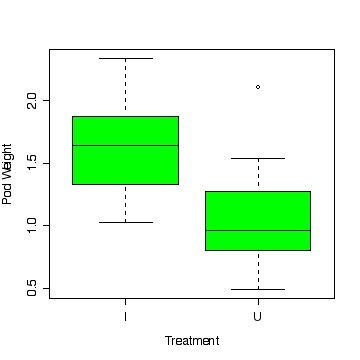
Data are taken from Table 8.28 on page 326 of Rosner, Fundamentals of Biostatistics, Fifth edition.
The purpose of this study was to demonstrate that soy beans inoculated with nitrogen-fixing bacteria grow adequately without the use of expensive and environmentally deleterious synthesized fertilizers.
> podwt <- data.frame(wt=c(1.76,1.45,1.03,1.53,2.34,1.96,1.79,1.21,0.49,0.85,1,1.54,1.01,0.75,2.11,0.92),
treat=factor(c(rep("I",8),rep("U",8))))
> podwt
wt treat
1 1.76 I
2 1.45 I
3 1.03 I
4 1.53 I
5 2.34 I
6 1.96 I
7 1.79 I
8 1.21 I
9 0.49 U
10 0.85 U
11 1.00 U
12 1.54 U
13 1.01 U
14 0.75 U
15 2.11 U
16 0.92 U
Compute mean, variance and standard deviation for the inoculated and uninoculated groups separately.
> sapply(split(podwt$wt,podwt$treat),mean)
I U
1.63375 1.08375
> sapply(split(podwt$wt,podwt$treat),var)
I U
0.1763125 0.2598839
> sqrt(sapply(split(podwt$wt,podwt$treat),var))
I U
0.4198958 0.5097881
> boxplot(split(podwt$wt,podwt$treat),xlab="Treatment",ylab="Pod Weight",col="green")

Use lm() to fit a Linear Model, and store the result in the lm object fitpodwt.
> fitpodwt <- lm(wt~treat, data=podwt)
summary() displays the fitted coeficients and their t-tests.
> summary(fitpodwt)
Call:
lm(formula = wt ~ treat, data = podwt)
Residuals:
Min 1Q Median 3Q Max
-0.60375 -0.25875 -0.09375 0.19875 1.02625
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.6338 0.1651 9.895 1.06e-07 ***
treatU -0.5500 0.2335 -2.355 0.0336 *
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.467 on 14 degrees of freedom
Multiple R-Squared: 0.2838, Adjusted R-squared: 0.2327
F-statistic: 5.548 on 1 and 14 DF, p-value: 0.03361
anova() displays the anova table.
> anova(fitpodwt)
Analysis of Variance Table
Response: wt
Df Sum Sq Mean Sq F value Pr(>F)
treat 1 1.2100 1.2100 5.548 0.03361 *
Residuals 14 3.0534 0.2181
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
There is some evidence (P = 0.034) from these data that the treatment is effective.