$R_0$, density thresholds, and eradication

1 R₀, density thresholds, and eradication

R₀ is a threshold for the ability of parasites to survive in a population. If R₀ < 1 then the disease can't persist in the population (even though the disease could still infect a few individuals, by chance, particularly if R₀ is nearly 1.0). We talked earlier about the general principle that S^* = N/R₀, which tells us that we can increase the number of susceptibles at equilibrium (and increase the number of healthy, uninfected individuals) by decreasing R₀. We can do this by

decreasing the contact rate b [better hygiene, changing behavior to avoid sources of infection such as streams, mosquito netting, condoms and clean needles, etc.]
increasing death or removal rate of infected individuals a [culling or quarantine]
increasing mortality rate of all individuals [culling]
increasing recovery rate

Two other ways to control disease are to lower the population density (another form of culling) and to vaccinate.

1.1 Density thresholds

R₀ is typically something like bN/(a+d+g); the contact rate is b (contacts per infected per susceptible per unit time), but the overall number of contacts per infective is bN. If the population, or the population density, goes down (we usually assume that we're dealing with epidemic dynamics in a fixed geographic region), then the contact rate goes down. If the population size/density is below a threshold value of N_T = (a+d+g)/b, then the population is too sparse for the disease to invade. This is one of the reasons, arguably, why many diseases were traditionally absent from less densely populated areas (see in particular William McNeill's Plagues and Peoples and Alfred Crosby's Ecological Imperialism. However, this argument doesn't entirely work: if R₀ was too small because the population density was too low, how come the diseases took off when they were introduced? (We might be able to come up with a story about evolution of virulence in dense populations, even though this is still something I don't fully understand ...)

1.2 Frequency-dependent thresholds

It's important to remember that the form of density-dependence built into simple SIR models is not the only way that disease can depend on population size and density. For example, in the vector-borne disease case that we discussed earlier, the number of vectors (female mosquitoes in the case of malaria) determines the upper limit of the contact rate: changing the number of hosts just dilutes the biting rate among more people. Another important case is what is called frequency-dependent transmission, where for one reason or another disease transmission depends on the frequency of infected individuals rather than the number. The clearest case here is sexually transmitted diseases; the number of sexual contacts per person remains roughly the same no matter how population density changes, so an infection rate of (bS I)/N is more appropriate than bS I.

More generally, what matters is how effective density (number of potentially infective contacts per individual per unit time) changes with population density. At one extreme, organisms that increase their interaction rate with density (behaving something like molecules in a simple chemical reaction) have purely density-dependent transmission. Organisms that adjust their behavior to keep the number of interactions the same regardless of population density have purely frequency-dependent transmission. With frequency-dependent transmission there is no density threshold; this is one (ecological) advantage to a parasite of being sexually transmitted when it lives in a sparse host population. Most organisms (including humans) are probably somewhere in between, and it is a major unresolved question exactly how to go about finding the data to answer the question. It's really important, too, because the change in interaction with density determines the answer to questions like: is there a threshold density? Can we eradicate disease through culling or vaccination? Which strategies are likely to work best?

1.3 Control by vaccination

Another way to control disease is to vaccinate. In the simplest case we suppose that we can vaccinate individuals with 100% effectiveness when they are born, and that they remain immune for the rest of their lives. If we draw a ``box model'' and write down equations for this, we see that the basic effect of vaccination is to lower the birth rate from the parasite's point of view: those individuals are being born, but they're progressing straight to the Recovered/Immune class without passing Go or collecting $200, and the parasites don't have a chance to infect them.

If we vaccinate a proportion p of the population at birth, the new R₀ drops to (1-p) times the old (pre-vaccination) R₀. If we want to eradicate the disease we need (1-p) R₀ < 1 or p > 1-1/R₀.
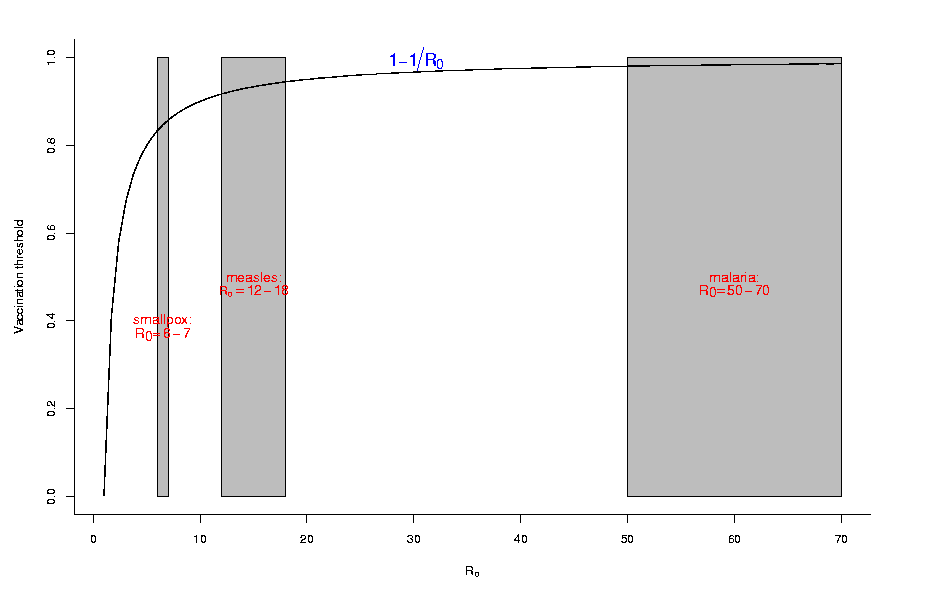
vaccination threshold curve

This has several immediate consequences:

We don't necessarily have to vaccinate every single person in the population to eradicate the disease completely. When enough individuals are vaccinated, we get what is called herd immunity; the contacts that infected individuals make with immune (vaccinated) individuals dilute the transmission process enough that the entire disease dies out.
How much we have to vaccinate depends critically on R₀. For example, smallpox (which is the only disease we have actually managed to eradicate) has R₀ ť 6-7, which means we need to vaccinate about 85% of the population. Measles has R₀ ť 10-15 - 90-93%. Malaria has R₀ > 50 by some estimates, which means we need to vaccinate more than 98% of the population! The curve gets really bad somewhere between smallpox and measles, and starts to crunch up against 1.0. And all of this doesn't take into account vaccine failure, hard-to-reach members or segments of the population, etc..
The algebraic argument above is simple enough that it also holds for other forms of prevention (such as blocking transmission through needle exchange or condoms). It continues to frustrate me personally that HIV/AIDS, which doesn't have that high an R₀ (possibly as low as 2 in some populations), is so hard to stop. If we could protect only 80% of the populations, we could wipe out the disease!

1.4 Stochastic thresholds and ``fade-out''

2 Conclusions

What does this mean for control? Vaccination, culling, prevention; having a vaccine won't necessarily do the job (although it helps a hell of a lot). Control vs eradication.

Other complications:

all the other things we left out of the model: genetic heterogeneity, population aggregation, etc. etc. etc.
reservoirs: zoonoses
persistent/recrudescing strains