In a broad sense, my primary research interests are mathematical modelling and scientific computing, with application in fluid dynamics, biology, and industry.

Uncovering realistic parameters in models of lithium-ion batteries

Using measurements from experiments performed by my collaborators, I am calculating the transport and diffusion coefficients of a multi-phase, multi-scale electrochemical model in order to achieve an accurate mathematical description of the chemical reactions in a lithium-ion battery.

Modelling polymorphic transformation of bacterial flagella during locomotion

We develop a model that describes the swimming technique performed by bacteria with multiple flagella, for example E. coli. These bacteria swim in their fluid environment by rotating helical flagella that are attached to their cell bodies. A cell propels forward by rotating its filaments counter-clockwise with each flagellum taking a left-handed helical shape. To change directions, one or more flagella will reverse its motor rotation which then changes the chirality of its helical form to right-handed. Using Kirchhoff Rode theory and Stokes equations, we develop a fluid-structure interaction model to describe flagella that are capable of taking on multiple stable helical configurations. Below are two simulations of a single flagellum that undergoes polymorphic transformation. On the left, the one end of the filament is fixed to a rotating motor point. A reversal in the motor rotation initiates a transformation to change the filament from a left-handed helix to a right-handed helix. On the right, one end of the filament is fixed in place and is subject to an external fluid flow. A sufficiently high fluid velocity generates a torque that causes a transformation. For more details, see our paper in Physical Review E (link).

              

Parametric resonance in spherical immersed elastic shells

In this project, I study parametric resonance in a class of fluid-structure systems where an elastic shell is immersed in an incompressible, viscous fluid. Parametric resonance refers to an instability that arises in a dynamical system due to periodic variations in a system parameter, which in this case is the elastic stiffness. The mathematical model is formulated in the immersed boundary framework to consider the two-way fluid-structure interaction between the elastic membrane and the surrounding fluid. A Floquet stability analysis shows that certain spatial modes of the membrane can be unstable at high Reynolds number. Below are animations that illustrate parametric instabilities. Each simulation uses the same physical parameters but are given different spatial perturbations. Over time we observe the growth of these perturbations. This work has been published in the SIAM Journal on Applied Mathematics (link) and a detailed analysis can be found in my Ph.D. thesis (link).

A model of the cochlea with parametric forcing

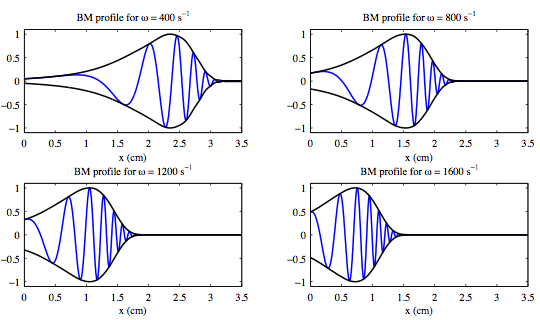
I explore the possibility of parametric resonance as a mechanism that contributes to the active process in the mammalian hearing system. The cochlea, or inner ear, is a fluid-filled, spiralled shell with membranes located along the interior. Travelling waves along the basilar membrane (BM) attain a localized peak which depends on the input sound frequency. This travelling wave phenomena gives the cochlea the ability hear and distinguish pitches. I examine a two-dimensional immersed boundary model of the cochlea with parametric forcing and show that an internally forced membrane can exhibit the travelling wave phenomena. Below is a figure of a parametrically forced BM at various forcing frequencies. A paper on this model has been published in the SIAM Journal on Applied Mathematics (link).

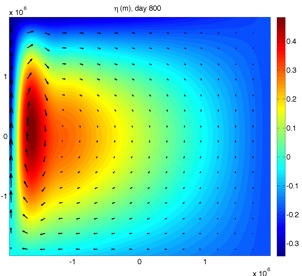
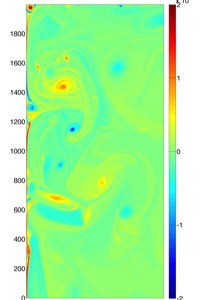
High-resolution simulations of wind-driven gyres

During my Master’s program, I developed a numerical method to study ocean dynamics at high temporal and spatial resolutions. The dynamics of the ocean occurs at a vast range of length and time scales which makes it a challenge to model and simulate. I used a spectral collocation scheme to simulate models in geophysical fluid dynamics at high resolution. The code was implemented with parallel capabilities which permits high temporal resolution while computing within a reasonable amount of time. A couple images from my simulations are below. The first image is a free surface plot of the rotating shallow water equations with external wind forcing. This particular simulation equilibrates to a laminar flow. A western intensification of the gyre flow is due to the rotation and curvature of the Earth and is observed in a real ocean, e.g. the Gulf stream. If we lower the eddy viscosity parameter, the flow becomes turbulent. The next image is a close-up of a turbulent flow. We observe dynamics that occur at much smaller length scales. In particular, the vortex shedding off the western boundary. A link to my Masters thesis can be found here (thesis link).