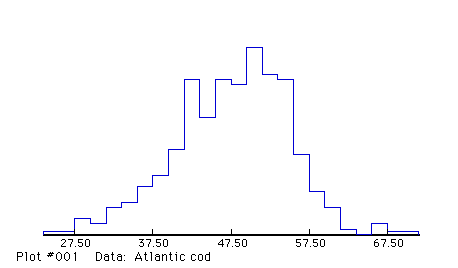
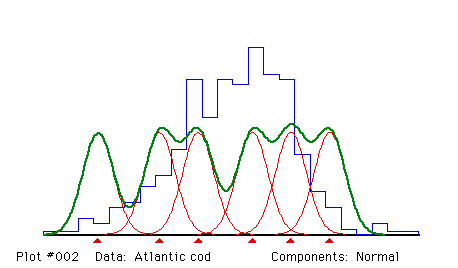
OPEN A SUBSAMPLING DATA FILE Title: Atlantic cod Number of intervals: 22 Number of components: 6 Do you want to continue reading this file (Y/N) ? y INTVL RGT BND SUM SUBSAMPLING DATA... Atlantic cod 1 27.500 1 1 0 0 0 0 0 2 29.500 3 3 0 0 0 0 0 3 31.500 2 2 0 0 0 0 0 4 33.500 3 3 0 0 0 0 0 5 35.500 3 2 1 0 0 0 0 6 37.500 3 0 1 2 0 0 0 7 39.500 3 0 1 2 0 0 0 8 41.500 3 0 2 1 0 0 0 9 43.500 3 0 0 3 0 0 0 10 45.500 3 0 0 2 1 0 0 11 47.500 3 0 0 2 1 0 0 12 49.500 3 0 0 1 0 2 0 13 51.500 3 0 0 1 1 1 0 14 53.500 3 0 0 1 0 1 1 15 55.500 3 0 0 1 1 1 0 16 57.500 3 0 0 0 2 1 0 17 59.500 3 0 0 0 1 1 1 18 61.500 3 0 0 1 0 1 1 19 63.500 1 0 0 0 1 0 0 20 65.500 0 21 67.500 2 0 0 0 0 2 0 22 1 0 0 0 0 0 1 READ A FULL SET OF PARAMETER VALUES How many components? NOTE: Must be at least 1, at most 15 6 Enter the 6 proportions: 1 1 1 1 1 1 Enter the 6 means: 30 38 43 50 55 60 Enter the 6 sigmas: 2 2 2 2 2 2 Proportions do not sum to 1. Do you want to re-scale (Y/N) ? y Proportions .16667 .16667 .16667 .16667 .16667 .16667 Means 30.0000 38.0000 43.0000 50.0000 55.0000 60.0000 Sigmas 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
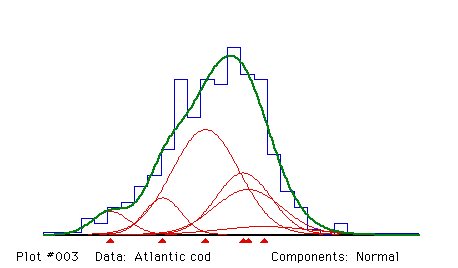
 FIT BY QUASI-NEWTON ALGORITHM AND/OR COMPUTE STANDARD ERRORS
>> Distribution selected: Normal
>> Subsampling data will be used
Enter iteration limit
[or 0 to get standard errors of current parameters]:
30
Display observed and expected counts (Y/N) ?
n
Display variance-covariance matrix (Y/N) ?
n
Constraints on proportions:
0 (NONE), 1 (SPECIFIED PROPORTIONS FIXED).
Enter choice:
0
Constraints on means:
0 (NONE), 1 (SPECIFIED MEANS FIXED),
2 (MEANS EQUAL), 3 (EQUALLY SPACED),
4 (GROWTH CURVE).
Enter choice:
0
Constraints on sigmas:
0 (NONE), 1 (SPECIFIED SIGMAS FIXED),
2 (FIXED COEF. OF VARIATION), 3 (CONSTANT COEF. OF VARIATION),
4 (SIGMAS EQUAL).
Enter choice:
0
Do you want to abort (Y/N) ?
n
Number of iterations = 18
Fitting Normal components
Proportions and their standard errors
.05365 .08139 .43178 .20584 .18538 .04196
.01498 .03075 .07179 .06278 .05995 .02731
Means and their standard errors
31.8358 39.7396 46.1947 51.8763 52.5712 54.9786
.9382 1.1127 .8288 1.1280 1.3936 3.5755
Sigmas and their standard errors
2.8551 2.7257 5.0369 4.0950 5.0538 6.6290
.7339 .7406 .4816 .6529 .7548 2.0990
Degrees of freedom = 22 - 1 + 126 - 21 - 17 - 21 = 88
Chi-squared = 50.7649 (P = .9995)
* WARNING * GOODNESS-OF-FIT TEST MAY BE INVALID; 85 EXPECTED COUNTS ARE < 1
FIT BY QUASI-NEWTON ALGORITHM AND/OR COMPUTE STANDARD ERRORS
>> Distribution selected: Normal
>> Subsampling data will be used
Enter iteration limit
[or 0 to get standard errors of current parameters]:
30
Display observed and expected counts (Y/N) ?
n
Display variance-covariance matrix (Y/N) ?
n
Constraints on proportions:
0 (NONE), 1 (SPECIFIED PROPORTIONS FIXED).
Enter choice:
0
Constraints on means:
0 (NONE), 1 (SPECIFIED MEANS FIXED),
2 (MEANS EQUAL), 3 (EQUALLY SPACED),
4 (GROWTH CURVE).
Enter choice:
0
Constraints on sigmas:
0 (NONE), 1 (SPECIFIED SIGMAS FIXED),
2 (FIXED COEF. OF VARIATION), 3 (CONSTANT COEF. OF VARIATION),
4 (SIGMAS EQUAL).
Enter choice:
0
Do you want to abort (Y/N) ?
n
Number of iterations = 18
Fitting Normal components
Proportions and their standard errors
.05365 .08139 .43178 .20584 .18538 .04196
.01498 .03075 .07179 .06278 .05995 .02731
Means and their standard errors
31.8358 39.7396 46.1947 51.8763 52.5712 54.9786
.9382 1.1127 .8288 1.1280 1.3936 3.5755
Sigmas and their standard errors
2.8551 2.7257 5.0369 4.0950 5.0538 6.6290
.7339 .7406 .4816 .6529 .7548 2.0990
Degrees of freedom = 22 - 1 + 126 - 21 - 17 - 21 = 88
Chi-squared = 50.7649 (P = .9995)
* WARNING * GOODNESS-OF-FIT TEST MAY BE INVALID; 85 EXPECTED COUNTS ARE < 1
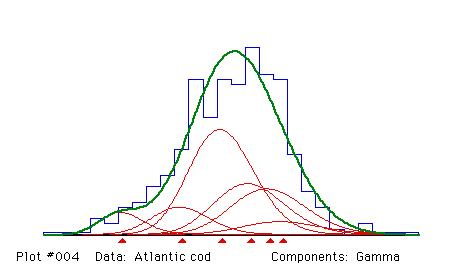
 CHOOSE A DISTRIBUTION
Distribution chosen: Gamma
FIT BY QUASI-NEWTON ALGORITHM AND/OR COMPUTE STANDARD ERRORS
>> Distribution selected: Gamma
>> Subsampling data will be used
Enter iteration limit
[or 0 to get standard errors of current parameters]:
30
Display observed and expected counts (Y/N) ?
n
Display variance-covariance matrix (Y/N) ?
n
Constraints on proportions:
0 (NONE), 1 (SPECIFIED PROPORTIONS FIXED).
Enter choice:
0
Constraints on means:
0 (NONE), 1 (SPECIFIED MEANS FIXED),
2 (MEANS EQUAL), 3 (EQUALLY SPACED),
4 (GROWTH CURVE).
Enter choice:
4
Is Kth mean different (Y/N) ?
n
Constraints on sigmas:
0 (NONE), 1 (SPECIFIED SIGMAS FIXED),
2 (FIXED COEF. OF VARIATION), 3 (CONSTANT COEF. OF VARIATION),
4 (SIGMAS EQUAL).
Enter choice:
3
Is Kth sigma different (Y/N) ?
n
Do you want to abort (Y/N) ?
n
Number of iterations = 15
Fitting Gamma components
Proportions and their standard errors
.05675 .08988 .39432 .20700 .19580 .05625
.01525 .03280 .06919 .06280 .05408 .02897
Means (ON A GROWTH CURVE) and standard errors
(Linf = 58.988; t1-t0 = 2.0795; k = .377258)
(s.e.: 3.990 .4117 .103497)
32.0693 40.5287 46.3297 50.3076 53.0354 54.9060
.9836 .7564 .6671
Sigmas (CONSTANT COEF. OF VAR. = .0996) and standard error
3.1942 4.0368 4.6146 5.0108 5.2825 5.4688
.2536
Degrees of freedom = 22 - 1 + 126 - 21 - 9 - 18 = 99
Chi-squared = 56.6878 (P = .9998)
* WARNING * GOODNESS-OF-FIT TEST MAY BE INVALID; 91 EXPECTED COUNTS ARE < 1
CHOOSE A DISTRIBUTION
Distribution chosen: Gamma
FIT BY QUASI-NEWTON ALGORITHM AND/OR COMPUTE STANDARD ERRORS
>> Distribution selected: Gamma
>> Subsampling data will be used
Enter iteration limit
[or 0 to get standard errors of current parameters]:
30
Display observed and expected counts (Y/N) ?
n
Display variance-covariance matrix (Y/N) ?
n
Constraints on proportions:
0 (NONE), 1 (SPECIFIED PROPORTIONS FIXED).
Enter choice:
0
Constraints on means:
0 (NONE), 1 (SPECIFIED MEANS FIXED),
2 (MEANS EQUAL), 3 (EQUALLY SPACED),
4 (GROWTH CURVE).
Enter choice:
4
Is Kth mean different (Y/N) ?
n
Constraints on sigmas:
0 (NONE), 1 (SPECIFIED SIGMAS FIXED),
2 (FIXED COEF. OF VARIATION), 3 (CONSTANT COEF. OF VARIATION),
4 (SIGMAS EQUAL).
Enter choice:
3
Is Kth sigma different (Y/N) ?
n
Do you want to abort (Y/N) ?
n
Number of iterations = 15
Fitting Gamma components
Proportions and their standard errors
.05675 .08988 .39432 .20700 .19580 .05625
.01525 .03280 .06919 .06280 .05408 .02897
Means (ON A GROWTH CURVE) and standard errors
(Linf = 58.988; t1-t0 = 2.0795; k = .377258)
(s.e.: 3.990 .4117 .103497)
32.0693 40.5287 46.3297 50.3076 53.0354 54.9060
.9836 .7564 .6671
Sigmas (CONSTANT COEF. OF VAR. = .0996) and standard error
3.1942 4.0368 4.6146 5.0108 5.2825 5.4688
.2536
Degrees of freedom = 22 - 1 + 126 - 21 - 9 - 18 = 99
Chi-squared = 56.6878 (P = .9998)
* WARNING * GOODNESS-OF-FIT TEST MAY BE INVALID; 91 EXPECTED COUNTS ARE < 1