A tale of two balloons and many cracks

In a classical experiment, two rubber ballons are connected by a pipe. Against all intuition, as on pumps air into the balloons, only one inflates (Weinhaus & Barker, 1978). This phenomenon can be explained by showing that the elastic energy \(\mathcal{E}(V_1,V_2)\) of a system consisting of two balloons with volumes \(V_1\) and \(V_2\) respectively is a non-convex function of \(V_1\) and \(V_2\) when \(V_1+V_2\) is large enough. The configuration minimizing \(\mathcal E\) under a total volume constraint \(V_1+V_2 = V\) is achieved by the configurations \(V_1=0\), \(V_2=V\) or \(V_1 = V\) and \(V_2=0\) while the configuration associated to two equally inflated balloons (\(V_1 =V_2 = V/2\)) is actually an unstable critical point of \(\mathcal E\).

In an article to appear in the International Journal of Fracture, (Tanné, Bourdin, & Yoshioka, 2022), E. Tanné, K. Yoshioka and I identified a similar behavior during the hydraulic stimulation of a network of parallel cracks. We show that the configuration consisting of growing networks of parallel cracks (a common assumption) is unstable, and that any perturbation will lead to a configuration where only one of the hydraulic crack will grow.

This result is significant in practice as it challenges common assumptions on the physical extends and location of hydraulic fractures, and the density of fracture networks created during fracking for geothermal energy, shale gas extraction, or carbon sequestration.

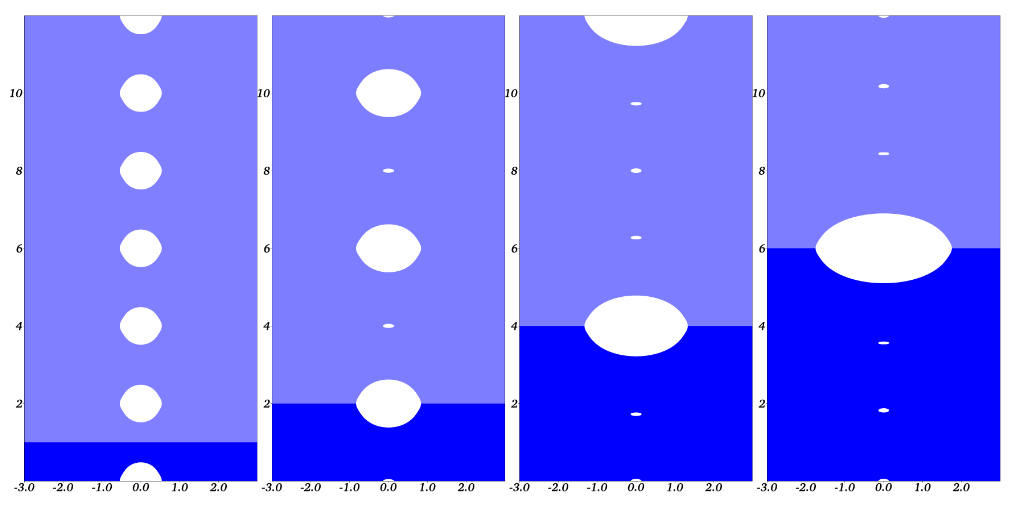
Loss of stability of a network of hydraulic crack configurations associated with an equal injection volume. The energy decreases with the number of growing cracks.

References

1. Weinhaus, F., & Barker, W. (1978). On the equilibrium states of interconnected bubbles or balloons. Am. J. Phys., 46(10), 978–982. DOI:10.1119/1.11487
2. Tanné, E., Bourdin, B., & Yoshioka, K. (2022). On the loss of symmetry in toughness dominated hydraulic fractures. Int. J. Fracture. DOI:10.1007/s10704-022-00623-5 Download