Defect Mechanics
Many of my research projects involve modeling and computer simulation of fine properties of materials in the context of defect mechanics and revolve around variational models and their implementation by “phase–fields”. The starting point of these approaches is the observation that Griffith’s criterion (Griffith, 1921) can be seen as a variational principle: the minimization of the sum of the mechanical and surface (fracture) energy with respect to the length of a single crack propagating along a known path (Francfort & Marigo, 1998), (Bourdin, Francfort, & Marigo, 2008). This principle can then be extended to that of successive minimizing the total energy
\[\begin{equation} \mathcal{E}(u,\Gamma) := \int_{\Omega\setminus\Gamma} W(\mathrm{e}(u))\, dx + G_c \mathcal{H}^{n-1}(\Gamma), \label{eq:defE} \end{equation}\]with respect to any kinematically admissible displacement field \(u\), and any crack set \(\Gamma\), subject to an irreversibility constraint, \(W(\mathrm{e}(u))\) denoting the strain energy density associated to the strain field \(\mathrm{e}(u)\), and \(G_c\) the critical elastic energy release rate, a material property.
Note that because it makes no assumption as to the actual geometry of the crack set \(\Gamma\) minimizing \(\mathcal{E}\), this problem provides the crack path de facto. Furthermore, it is possible to show that in situation where Griffith criterion applies, it is satisfied by the solutions of this problem. In short, variational models of brittle fracture generalize Griffith criterion without any assumption on the crack path, and are naturally capable of handling important features of hydraulic fracturing, such as new crack nucleation, propagation in heterogeneous media, or interaction between propagating or pre-existing cracks. They also require specific numerical tools.
In the “phase–field” methods, which I pioneered several years ago (Bourdin, 1998), (Bourdin, Francfort, & Marigo, 2000), (Bourdin, 2007), cracks are represented by a smooth “damage” variable \(\alpha\), depending on a regularization length \(\ell\), and the energy \(\mathcal{E}\) is approximated by
\[\begin{equation} \label{eq:defEl} \mathcal{E}_\ell(u,\alpha) = \int_\Omega a(\alpha)W(\mathrm{e}(u))\, dx + \frac{G_c}{4c_w} \int\frac{w(\alpha)}{\ell} + \ell|\nabla \alpha|^2\, dx, \end{equation}\]where \(a\) is a continuous non-negative function such that \(a(0)=1\), \(a(1)= 0\), \(w\) is a monotonously increasing function such that \(w(0) = 0\) and \(w(1) = 1\), and \(c_w = \int_0^1w(s)^{1/2}\, dx\) is a normalization parameter.
The energy \(\mathcal{E}_\ell\) is then iteratively minimized under the irreversibility constraint that \(\alpha\) is a non-decreasing function of time. Typically, this is achieved by iteratively minimizing \(\mathcal{E}_\ell\) with respect to \(u\) and \(\alpha\), using unstructured parallel finite elements, such as mef90/vDef, my reference implementation based on PETSc, or this one by C. Maurini, based on FEnics.
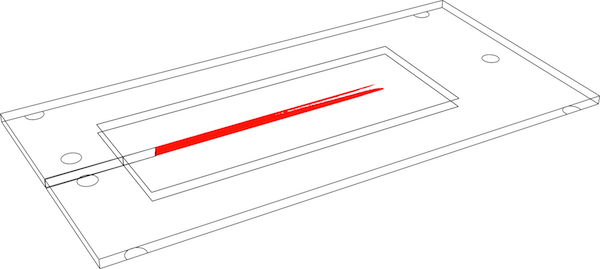
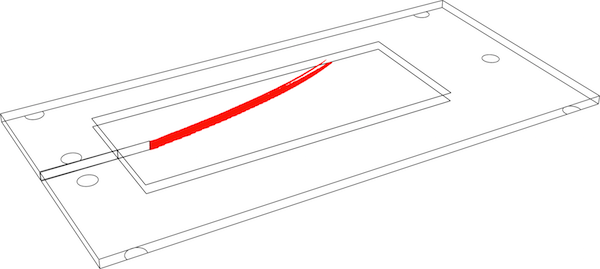
Numerical simulation of a double torsion experiment (Tait, Fry, & Garrett, 1987), (Madjoubi, Hamidouche, Bouaouadja, Chevalier, & Fantozzi, 2007). Crack deviation due to misaligned testing fixture or sample placement can be accurately predicted using this approach.
References
- Griffith, A. A. (1921). The phenomena of rupture and flow in solids. Philos T R Soc S-A, XXXXI(587), 163–198. DOI:10.1098/rsta.1921.0006
- Francfort, G. A., & Marigo, J.-J. (1998). Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids., 46(8), 1319–1342. DOI:10.1016/S0022-5096(98)00034-9
- Bourdin, B., Francfort, G. A., & Marigo, J.-J. (2008). The Variational Approach to Fracture. J. Elasticity, 91(1-3), 1–148. DOI:10.1007/s10659-007-9107-3 Download
- Bourdin, B. (1998). Une méthode variationnelle en mécanique de la rupture, théorie et applications numériques (PhD thesis). Université Paris Nord, Institut Galilée, France. Download
- Bourdin, B., Francfort, G. A., & Marigo, J.-J. (2000). Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids, 48(4), 797–826. DOI:10.1016/S0022-5096(99)00028-9 Download
- Bourdin, B. (2007). Numerical implementation of a variational formulation of quasi-static brittle fracture. Interfaces Free Bound., 9, 411–430. DOI:10.4171/IFB/171 Download
- Tait, R. B., Fry, P. R., & Garrett, G. G. (1987). Review and evaluation of the double-torsion technique for fracture toughness and fatigue testing of brittle materials. Exp. Mech., 27(1), 14–22. DOI:10.1007/BF02318858
- Madjoubi, M. A., Hamidouche, M., Bouaouadja, N., Chevalier, J., & Fantozzi, G. (2007). Experimental evaluation of the double torsion analysis on soda-lime glass. J. Mater. Sci., 42(18), 7872–7881. DOI:10.1007/s10853-007-1660-4
