Fracture of thin films
Fracture and debonding of thin coatings is a common engineering problem encountered in a wide range of problems including thermal barrier coatings, dry lubricants, or flexible integrated circuits. Whereas progress has been made in the analysis of such problems (Hutchinson & Suo, 1992), their numerical simulation is still challenging due to the very high aspect ratio of the domains involved.
In a conventional finite element mesh, resolving the stiffness of the film and properly approximating the displacements requires very small and high order elements, leading to a very high computational cost.
This problem has been the scope of a large international collaborative project with Jean-Jacques Marigo (École Polytechnique, France), Corrado Maurini and Jean-François Babadjian (Université Pierre et Marie Curie, France), Duvan Henao (Pontificia Universidad Católica de Chile), and then graduate students Andres León-Baldelli (Université Pierre et Marie Curie, France) and Ataollah Mesgarnejad (LSU). We derived an asymptotic two–dimensional model, using the techniques of dimension reduction, for the in-plane deformations and fracture of a thin film bonded to an elastic substrate through an elastic bonding layer (León-Baldelli, Babadjian, Bourdin, Henao, & Maurini, 2014), studied its properties (León-Baldelli, Bourdin, Marigo, & Maurini, 2013), then extended the model for out-of-plane deformations (Mesgarnejad, Bourdin, & Khonsari, 2013).
We were able to prove that the behavior of the film is governed by its elastic properties, a cohesive stiffness parameter \(k\) depending on the thickness and shear modulus of the bonding layer, the film’s fracture toughness \(G_f\), and an interfacial toughness \(G_d\) which can be computed explicitly from the geometric and material properties. Namely, if \(u_0\) denotes the boundary displacement of the substrate, \(\omega\) the two-dimensional film, \(D\) an unknown debonded region, and \(\Gamma\) an unknown set of transverse cracks, the three dimensional fracture energy reduces to
\[\begin{equation} \mathcal{F}(u,\Gamma,D) : = \int_{\omega \setminus \Gamma} W(\mathrm{e}(u))\, dx + k \int_{\omega \setminus D} (u-u_0)^{2}\, dx + G_f\mathcal{H}^{n-1}(\Gamma) + G_b|D|, \label{eq:ThinFilmEnergy} \end{equation}\]and can be approximated by the phase–field functional:
\[\begin{multline*} \mathcal{F}_\ell(u,\alpha,\delta) : = \int_{\omega} (1-\alpha)^{2} W(\mathrm{e}(u))\, dx + k \int_{\omega} (1-\delta)(u-u_0)^{2}\, dx \\ + \frac{G_f}{2}\int_\omega \frac{\alpha^{2}}{\ell} +\ell |\nabla \alpha|^2\, dx + G_b \int_\omega \delta\, dx, \label{eq:ThinFilmEnergyEps} \end{multline*}\]where \(\delta\) is a function taking its values in \((0,1)\), 0 and 1 representing respectively the perfectly bonded and fully debonded regions of the film.
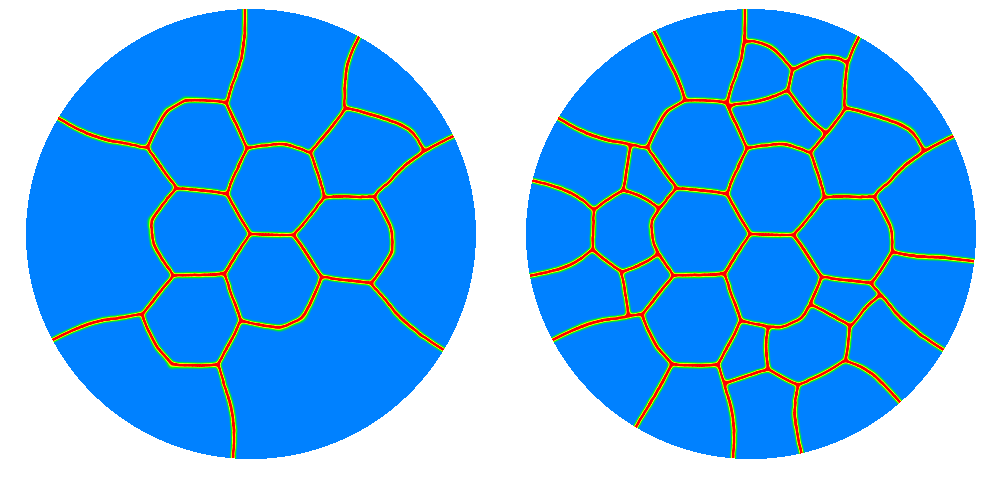
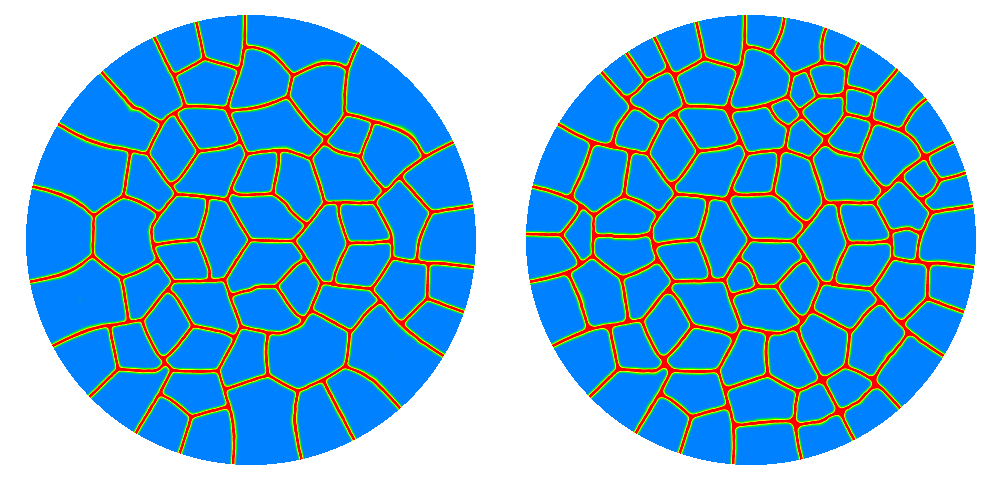
Numerical simulation of an elastic wafer coated by a brittle film, subject to an isotropic expansion, taken from (León-Baldelli, Babadjian, Bourdin, Henao, & Maurini, 2014). The fracture pattern exhibits features observed in nature such as the nucleation of near hexagonal “cells” and triple “Y” junctions at 120 degrees, followed by further subdivision leading to “T” junctions.

Numerical simulation of a nano-indentation experiment from (Mesgarnejad, Bourdin, & Khonsari, 2013).
References
- Hutchinson, J. W., & Suo, Z. (1992). Mixed Mode Cracking in Layered Materials. Adv. Appl. Mech., 29, 63–191.
- León-Baldelli, A. A., Babadjian, J.-F., Bourdin, B., Henao, D., & Maurini, C. (2014). A Variational Model For Fracture And Delamination Of Thin Films. J. Mech. Phys. Solids, 70, 15–32. DOI:10.1016/j.jmps.2014.05.020 Download
- León-Baldelli, A. A., Bourdin, B., Marigo, J.-J., & Maurini, C. (2013). Fracture and debonding of a thin film on a stiff substrate: analytical and numerical solutions of a 1d variational model. Cont. Mech. Thermodyn., 25(2-4), 243–268. DOI:10.1007/s00161-012-0245-x Download
- Mesgarnejad, A., Bourdin, B., & Khonsari, M. M. (2013). A variational approach to the fracture of brittle thin films under out of plane loading. J. Mech. Phys Solids, 61(11), 2360–2379. DOI:10.1016/j.jmps.2013.05.001 Download
RESEARCH
defectmechanics
