Image Processing
A segmentation of an image is “close” to the original one but also “homogeneous” far from some edges. Some compare this work to that of a cartoonist who would first sketch a set of contour lines and fill them with flat greys.
Of course, there are several way to achieve a segmentation and D. Mumford and J. Shah (Mumford & Shah, 1989) that for any given image whose grey level correspond to a function \(g\), one can compute a segmentation by minimizing amongst every edge set \(K\) and every segmented image \(u\) the energy functional:
\[\mathcal{E}(u,K) = \int_{\Omega \setminus K} |\nabla u|^2\, dx + \alpha \mathcal{H}^{N-1}(K\cap \Omega) + \beta\int_\Omega|u-g|^2\, dx,\]where, \(\alpha\) and \(\beta\) are two strictly positive parameters and \(\mathcal{H}^{N-1}\) denotes the \(N-1\)-dimensional Hausdorff measure (i.e. length in 2D or surface area in 3D).
The analysis and the numerical implementation of the Mumford-Shah problem are very challenging, mostly due to the nature of the unknowns: a function and a curve. Typically, the first step is to propose a weak formulation by identifying the edges and the discontinuities of the function \(u\) and defining the functional
\[E(u) = \int_{\Omega} |\nabla u|^2\, dx + \alpha \mathcal{H}^{N-1}(J_u) + \beta\int_\Omega|u-g|^2\, dx,\]where \(u\) now belongs to the space \(SBV(\Omega)\) of functions with bounded variations and \(J_u\) denotes its jump set.
Unfortunately, the numerical implementation of \(E\) is still challenging. Most classical numerical methods will not allow the direct approximation of arguments in \(SBV\), and one still has to approximate surface and bulk energies. There are many way to deal with this issue, two of which are presented below.
Approximation by the Ambrosio-Tortorelli functional
L. Ambrosio and V.M. Tortorelli suggested to approximate the Mumford-Shah energy by sequences of elliptic functionals, in the sense of the \(\Gamma\)-convergence (Ambrosio & Tortorelli, 1990), (Ambrosio & Tortorelli, 1992). Introducing a secondary variable v and a small parameter \(\varepsilon\), they showed that the functional
\[E_\varepsilon(u,v) = \int_\Omega (v^2 + \sqrt{\varepsilon})|\nabla u|^2\, dx + \alpha \int_\Omega \frac{(1-v)^2}{4\varepsilon} + \varepsilon|\nabla v|^2\, dx + \beta \int_\Omega(u-g)^2\, dx\]\(\Gamma\)-converges to the Mumford-Shah weak energy \(E\). In particular, this implies that the minimizers of the regularized functional converge in some sense to that of the original problem. This result can be further extended to the case of a finite element approximation of the original energy, provided that the mesh size \(h\) goes to 0 faster than the regularization parameter (Bellettini & Coscia, 1994), (Bourdin, 1999). This is the base of the numerical experiment presented below. From left to right, the figures represent the original image \(g\), the regularized edge set \(v\), and the segmented image \(u\).



Image segmentation using the Ambrosio-Tortorelli approximation of the Mumford-Shah functional, from (Bourdin, 1999).
###Adaptive Finite Element approximation
Another approach was first presented in (Chambolle & Dal Maso, 1999) then extended and implemented in (Bourdin & Chambolle, 2000). It relies again on finite elements, but requires the construction of an adapted mesh, in order to build a proper approximation of the discontinuous function (u). The following set of figure illustrate the construction of the adapted triangulation and the segmentation on the constructed mesh. The first row of figure correspond to a first segmentation and edge set on a background triangulation, and the second one present the same fields, and the final triangulation.


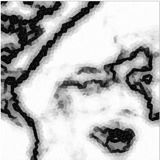
Image segmentation using an adaptive finite element approximation of the Mumford-Shah functional, from (Bourdin & Chambolle, 2000). Background mesh and segmentation
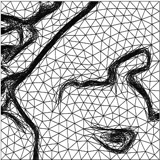
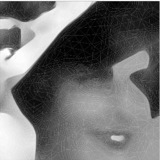
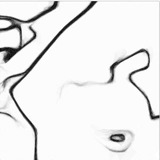
Image segmentation using an adaptive finite element approximation of the Mumford-Shah functional, from (Bourdin & Chambolle, 2000). Adapted mesh and segmentation
References
- Mumford, D., & Shah, J. (1989). Optimal approximation by piecewise smooth functions and associated variational problem. Comm. Pure. Appl. Math., 42, 577–685.
- Ambrosio, L., & Tortorelli, V. M. (1990). Approximation of functionals depending on jumps by elliptic functionals via Γ-convergence. Comm. Pure Appl. Math., 43(8), 999–1036.
- Ambrosio, L., & Tortorelli, V. M. (1992). On the approximation of free discontinuity problems. Boll. Un. Mat. Ital. B (7), 6(1), 105–123.
- Bellettini, G., & Coscia, A. (1994). Discrete approximation of a free discontinuity problem. Numer. Funct. Anal. Optim., 15(3-4), 201–224.
- Bourdin, B. (1999). Image segmentation with a finite element method. M2AN Math. Model. Numer. Anal., 33(2), 229–244. DOI:10.1051/m2an:1999114 Download
- Chambolle, A., & Dal Maso, G. (1999). Discrete approximations of the Mumford-Shah functional in dimension two. M2AN Math. Model. Num. Ana., 33(4), 651–672.
- Bourdin, B., & Chambolle, A. (2000). Implementation of an adaptive finite-element approximation of the Mumford-Shah functional. Numer. Math., 85(4), 609–646. DOI:10.1007/PL00005394 Download
