Fracture of heterogeneous media
It is well known that layering brittle materials, can be an effective toughening mechanism (Evans & Faber, 1981), as observed in sea-shells (Evans et al., 2001). With the rapid rise of “unconventional” energy resources and its strong reliance on hydraulic fracturing, a better understanding of fracture properties of heavily stratified rocks such as gas shales is in order. In particular, understanding how spatial variations of elastic moduli and fracture toughness across layers affects the “effective toughness” of rocks at the reservoir is required in order to conduct numerical simulations.
The idea of the “surfing boundary condition” is to guide the large scale propagation direction of a crack, while letting it be guided by the micro-geometry at the microscopic scale. The main idea is to apply a translating displacement of the form \(u(x,y) = U(x-t,y)\), where \(U\) is for example the mode-I \(K\)–dominant displacement
\[\begin{equation} \left\{\begin{array}{rcl} U_x(x,y) &=& \frac{K_I}{2\mu}\sqrt{\frac{r}{2\pi}}(\kappa-\cos\theta)\cos\tfrac{\theta}{2}\\ U_y(x,y) &=& \frac{K_I}{2\mu}\sqrt{\frac{r}{2\pi}}(\kappa-\cos\theta)\sin\tfrac{\theta}{2}, \end{array} \right. \label{eq:SurfingBC} \end{equation}\]\((r,\theta)\) being the polar coordinate emanating at the origin, and \(\kappa\) and \(\mu\) the effective bulk and shear modulus of the microstructured material considered. After computing the crack geometry for this boundary displacement, using a “phase–field” model of fracture, one can compute the crack tip energy flow with a classical \(J\)–integral. From this transient quantity, we can estimate the magnitude of the loading required to attain a steady state, which in turn we relate to the effective toughness of the considered microstructure (Hossain, Hsueh, Bourdin, & Bhattacharya, 2014).
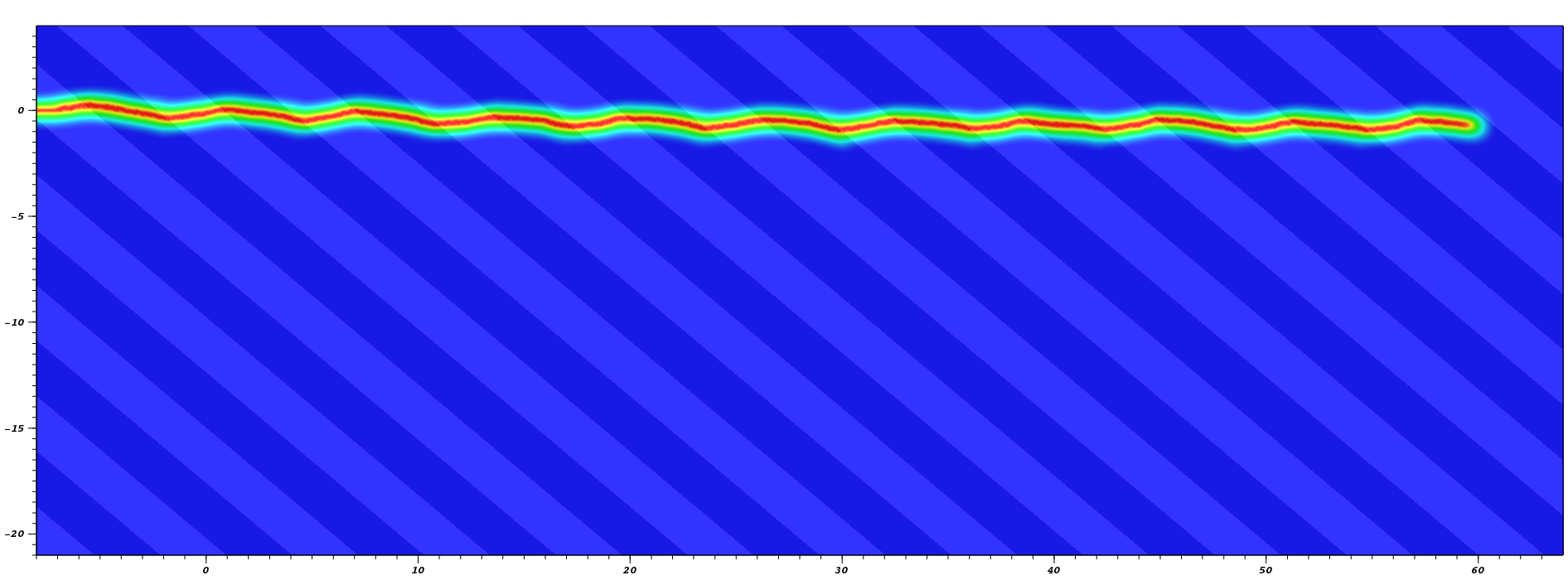

Surfing experiment on a layered material with respective normalized Young’s modulus \(1.3E_0\) and \(.7E_0\), and identical fracture toughness at an angle of 40 degree from (Hossain, Hsueh, Bourdin, & Bhattacharya, 2014). Crack path and time history of the energy flow, from which we estimate a toughening of over 20%
A natural next step is to leverage technique of optimal design to design microstructured materials with optimal fracture properties. This is the scope of an ongoing project in collaboration with K. Bhattacharya, G. Ravichandran and K. Faber (Caltech), supported by a grant from the DMREF program of the National Science Foundation
References
- Evans, A. G., & Faber, K. T. (1981). Toughening Of Ceramics By Circumferential Microcracking. J. Am. Ceram. Soc., 64, 394–398. DOI:10.1111/j.1151-2916.1981.tb09877.x
- Evans, A. G., Suo, Z., Wang, R. Z., Aksay, I. A., He, M. Y., & Hutchinson, J. W. (2001). Model for the robust mechanical behavior of nacre. J. Mater. Res., 16, 2475–2484. DOI:10.1557/JMR.2001.0339
- Hossain, M. Z., Hsueh, C.-J., Bourdin, B., & Bhattacharya, K. (2014). Effective toughness of heterogeneous media. J. Mech. Phys. Solids, 71, 320–348. DOI:10.1016/j.jmps.2014.06.002 Download
More pages on this topic
RESEARCH
defectmechanics
