Thermal shock
The thermal shock of a brittle medium often leads to the nucleation of periodic arrays of cracks, and the selective arrest of some cracks at the expense of others (Bahr, Fischer, & Weiss, 1986), (Geyer & Nemat-Nasser, 1982), (Jiang et al., 2012), (Shao et al., 2010), (Shao et al., 2011). Modeling the morphogenesis and propagation of such complex fracture networks has been the subject of intense studies and is still a major challenge. When the impact of the developing cracks on heat transfer is neglected, accounting for thermal stress in a phase–field setting is as simple as solving a heat transfer problem for the temperature field \(\theta\), and replacing the strain energy density \(W(\mathrm{e}(u))\) in \(\mathcal{E}\) and \(\mathcal{E}_\ell\) by a thermoelastic energy density \(W(\mathrm{e}(u),\theta)\).
One of the main difficulties in the modeling and simulation of this experiment is handling crack nucleation without elastic singularity, which is impossible in Griffith’ theory. A joint project with C. Maurini (Universite Pierre et Marie Curie, France), J.-J. Marigo (École Polytechnique, France), and graduate student P. Sicsic, then supported by Lafarge, leveraged the dual nature of \(\mathcal{E}_\ell\), seen as an approximation of a fracture energy at the structural scale and as a gradient damage model at the scale of \(\ell\) (Sicsic, Marigo, & Maurini, 2013). Using this approach, we closely matched experimental observations from (Shao et al., 2011).
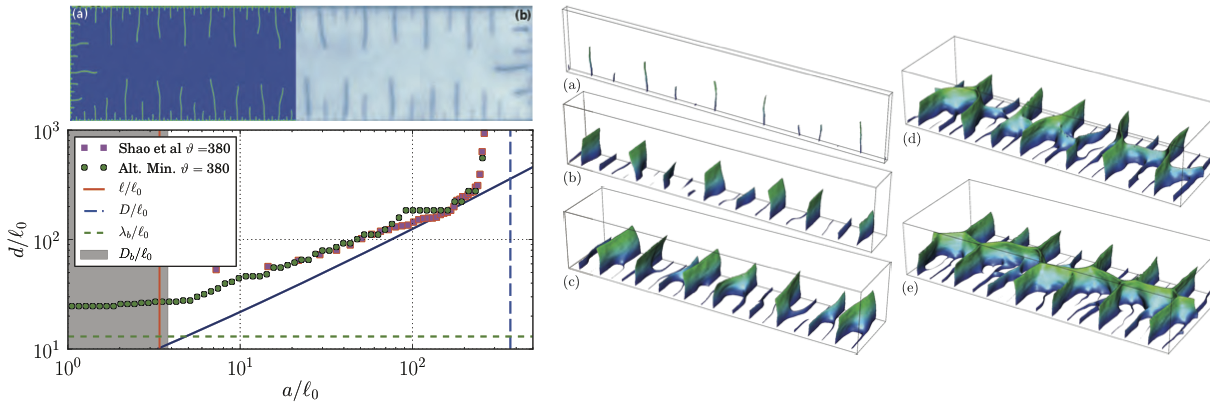
Numerical simulations from (Bourdin, Marigo, Maurini, & Sicsic, 2014). Computed and observed crack geometry. Crack spacing as a function of the distance to the edge of the sample are compared to experiments and a scaling law from the literature. Evolution of the fracture pattern in a thermal shock at given temperature in samples of thickness 0.1, 0.5, 1, and 2mm
Large numerical simulation of thermal shock of a three-dimensional body from (Bourdin, Marigo, Maurini, & Sicsic, 2014), performed on 1,536 cores on the Stampede supercomputer at TACC with domain discretized by approximately 65,000,000 elements. See videos on youtube here and here.
The qualitative behavior of crack patterns delimiting near hexagonal “cells” and gradually coalescing match observations.
Cracks “cell” size and geometry plotted against the distance to the exposed face over 5 orders of magnitude, compared with the scaling law of (Bahr et al., 2010).
References
- Bahr, H.-A., Fischer, G., & Weiss, H.-J. (1986). Thermal-shock crack patterns explained by single and multiple crack propagation. J. Mater. Sci., 21(8), 2716–2720. DOI:10.1007/BF00551478
- Geyer, J. F., & Nemat-Nasser, S. (1982). Experimental Investigations of Thermally Induced Interacting Cracks in Brittle Solids. Int. J. Solids Structures, 18(4), 137–356. DOI:10.1016/0020-7683(82)90059-2
- Jiang, C. P., Wu, X. F., Li, J., Song, F., Shao, Y. F., Xu, X. H., & Yan, P. (2012). A study of the mechanism of formation and numerical simulations of crack patterns in ceramics subjected to thermal shock. Acta Materialia, 60(11), 4540–4550. DOI:10.1016/j.actamat.2012.05.020
- Shao, Y., Xu, X., Meng, S., Bai, G., Jiang, C., & Song, F. (2010). Crack Patterns in Ceramic Plates after Quenching. J. Am. Ceram. Soc., 93(10), 3006–3008. DOI:10.1111/j.1551-2916.2010.03971.x
- Shao, Y., Zhang, Y., Xu, X., Zhou, Z., Li, W., & Liu, B. (2011). Effect of Crack Pattern on the Residual Strength of Ceramics After Quenching. J. Am. Ceram. Soc., 94(9), 2804–2807. DOI:10.1111/j.1551-2916.2011.04728.x
- Sicsic, P., Marigo, J.-J., & Maurini, C. (2013). Initiation of a periodic array of cracks in the thermal shock problem: a gradient damage modeling. J. Mech. Phys. Solids, 63, 256–284. DOI:10.1016/j.jmps.2013.09.003
- Bourdin, B., Marigo, J.-J., Maurini, C., & Sicsic, P. (2014). Morphogenesis and Propagation of Complex Cracks Induced by Thermal Shocks. Phys. Rev. Lett., 112(1), 014301. DOI:10.1103/PhysRevLett.112.014301 Download
- Bahr, H. A., Weiss, H. J., Hofmann, U. B., M., Fischer, G., Lampenscherf, S., & Balke, H. (2010). Scaling behavior of thermal shock crack patterns and tunneling cracks driven by cooling or drying. J. Mech. Phys. Solids, 58(9), 1411–1421. DOI:10.1016/j.jmps.2010.05.005
RESEARCH
defectmechanics
